Różnica między testem t a ANOVA

- 893
- 199
- Salwator Słowiński
 Istnieje cienka linia rozgraniczenia pośród testu t i anva, i.mi. Gdy należy porównać średnie populacyjne wynoszące tylko dwie grupy, Test t jest używany, ale gdy należy porównać środki więcej niż dwie grupy, ANOVA jest preferowany.
Istnieje cienka linia rozgraniczenia pośród testu t i anva, i.mi. Gdy należy porównać średnie populacyjne wynoszące tylko dwie grupy, Test t jest używany, ale gdy należy porównać środki więcej niż dwie grupy, ANOVA jest preferowany.
Test t i analiza wariancji skróconej jako ANOVA, to dwie parametryczne techniki statystyczne stosowane do przetestowania hipotezy. Ponieważ są one oparte na wspólnym założeniu, takim jak populacja, z której pobierana jest próbka, powinna być normalnie rozmieszczona, jednorodność wariancji, losowe próbkowanie danych, niezależność obserwacji, pomiar zmiennej zależnej na stosunku lub poziomie przedziału, ludzie często źle interpretują te dwa.
Tutaj przedstawiono artykuł, aby zrozumieć znaczącą różnicę między testem t a ANOVA, wyglądać.
Treść: Test t VS ANOVA
- Wykres porównania
- Definicja
- Kluczowe różnice
- Wniosek
Wykres porównania
| Podstawa do porównania | Test t | ANOVA |
|---|---|---|
| Oznaczający | Test t jest testem hipotezy, który służy do porównania środków dwóch populacji. | ANOVA to technika statystyczna, która służy do porównania środków więcej niż dwóch populacji. |
| Statystyka testowa | (x ̄-µ)/(s/√n) | Między wariancją próbki/w obrębie wariancji próbki |
Definicja testu t
Test t opisany jako test statystyczny, który bada, czy średnie populacyjne dwóch próbek znacznie się różnią, stosując dystrybucję T, która jest stosowana, gdy odchylenie standardowe nie jest znane, a wielkość próby jest niewielka. Jest to narzędzie do analizy, czy dwie próbki są pobierane z tej samej populacji.
Test opiera się na statystyce T, która zakłada, że zmienna jest normalnie rozmieszczona (symetryczny rozkład w kształcie dzwonu), a średnia jest znana, a wariancja populacji oblicza się z próbki.
W testach zerowych zerowych przybiera formę H0: µ (x) = µ (y) przeciwko alternatywnej hipotezie h1: µ (x) ≠ µ (y), w których µ (x) i µ (y) reprezentują średnie populacyjne. Stopień wolności testu T wynosi n1 + N2 - 2
Definicja ANOVA
Analiza wariancji (ANOVA) jest metodą statystyczną, powszechnie stosowaną we wszystkich tych sytuacjach, w których należy dokonać porównania między więcej niż dwoma środkami populacyjnymi, takimi jak wydajność upraw z wielu odmian nasion. Jest to istotne narzędzie analizy dla badacza, które pozwala mu przeprowadzać test jednocześnie. Kiedy używamy ANOVA, zakłada się, że próbka jest pobierana z normalnie rozłożonej populacji, a wariancja populacji jest równa.
W ANOVA całkowita zmienność zestawu danych jest podzielona na dwa typy, i.mi. Kwota przydzielona na przypadek i kwotę przypisaną do konkretnych przyczyn. Jego podstawową zasadą jest przetestowanie wariancji między średnimi populacji poprzez ocenę zmienności w pozycjach grupowych, proporcjonalnie do ilości zmienności między grupami. W próbce wariancja wynika z losowego niewyjaśnionego zaburzenia, podczas gdy inne leczenie może powodować między wariancją próbki.
Przy użyciu tej techniki testujemy, zerowa hipoteza (h0), w którym wszystkie środki populacji są takie same lub alternatywna hipoteza (h1), w którym co najmniej jedna populacja jest inna.
Kluczowe różnice między testem t i ANOVA
Istotne różnice między testem t i ANOVA są szczegółowo omówione w następujących punktach:
- Test hipotezy, który służy do porównania środków dwóch populacji, nazywa się testem t. Technika statystyczna, która służy do porównania środków więcej niż dwóch populacji, jest znana jako analiza wariancji lub ANOVA.
- Statystyka testu dla testu t jest:
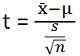 Statystyka testowa dla ANOVA to:
Statystyka testowa dla ANOVA to: 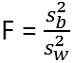
Wniosek
Po przejrzeniu powyższych punktów można powiedzieć, że test t jest specjalnym rodzajem ANOVA, którego można użyć, gdy mamy tylko dwie populacje do porównania ich środków. Chociaż szanse na błędy mogą wzrosnąć, jeśli test t zostanie użyty, gdy musimy jednocześnie porównać więcej niż dwa środki populacji, dlatego stosuje się ANOVA
- « Różnica między otwartymi i zamkniętymi funduszami inwestycyjnymi
- Różnica między zwykłą rentą a rentą należną »

