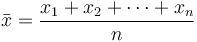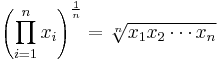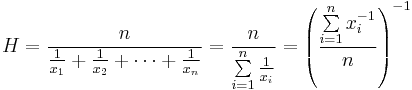Średnia vs. Mediana
- 4419
- 1261
- Łukasz Kalisz
Mieć na myśli (lub średnio) i mediana są terminami statystycznymi, które odgrywają nieco podobną rolę w zakresie zrozumienia tendencji centralnej zbioru wyników statystycznych. Chociaż średnia tradycyjnie była popularną miarą środkowego punktu w próbie, ma wadę, jaką jest to, że dowolna pojedyncza wartość jest zbyt wysoka lub zbyt niska w porównaniu z resztą próbki. Właśnie dlatego mediana jest czasem traktowana jako lepsza miara punktu środkowego.
Wykres porównania
| Mieć na myśli | Mediana | |
|---|---|---|
| Definicja | Średnia jest średnia arytmetyczna zestawu liczb lub dystrybucji. Jest to najczęściej stosowana miara centralnej tendencji zestawu liczb. | Mediana jest opisana jako wartość liczbowa oddzielająca wyższą połowę próbki, populację lub rozkład prawdopodobieństwa, od dolnej połowy. |
| Zastosowanie | Średnia jest używana do normalnych rozkładów. | Mediana jest ogólnie stosowana do wypaczonych rozkładów. |
| Znaczenie dla zestawu danych | Średnia nie jest solidnym narzędziem, ponieważ ma na to w dużej mierze wpływ. | Mediana lepiej nadaje się do wypaczonych rozkładów do uzyskania tendencji centralnej, ponieważ jest znacznie bardziej solidna i rozsądna. |
| Jak obliczyć | Średnia jest obliczana przez dodanie wszystkich wartości i podzielenie tego wyniku przez liczbę wartości. | Mediana to liczba znaleziona na dokładnym środku zestawu wartości. Medianę można obliczyć, wymieniając wszystkie liczby w kolejności rosnącej, a następnie zlokalizując liczbę w środku tego rozkładu. |
Definicje średniej i mediany
W matematyce i statystyce średniej lub Średnia arytmetyczna listy liczb to suma całej listy podzielonej przez liczbę elementów na liście. Patrząc na rozkłady symetryczne, średnia jest prawdopodobnie najlepszą miarą, aby osiągnąć tendencję centralną. W teorii prawdopodobieństwa i statystyki A, a mediana Czy ta liczba oddziela wyższa połowa próbki, populacja lub rozkład prawdopodobieństwa, od dolnej połowy.
Jak obliczyć
Mieć na myśli lub średnia jest prawdopodobnie najczęściej stosowaną metodą opisu tendencji centralnej. Średnia jest obliczana przez dodanie wszystkich wartości i podzielenie tego wyniku przez liczbę wartości. Średnia arytmetyczna próbki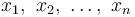 
jest sumą próbkowanych wartości podzielonych przez liczbę elementów w próbce:
Mediana to liczba znaleziona na dokładnym środku zestawu wartości. Medianę można obliczyć, wymieniając wszystkie liczby w kolejności rosnącej, a następnie zlokalizując liczbę w środku tego rozkładu. Ma to zastosowanie do listy numerów nieparzystych; W przypadku równej liczby obserwacji nie ma pojedynczej wartości środkowej, więc zwykłą praktyką jest przyjmowanie średniej z dwóch środkowych wartości.
Przykład
Powiedzmy, że w klasie jest dziewięciu uczniów z następującymi wynikami na teście: 2, 4, 5, 7, 8, 10, 12, 13, 83. W tym przypadku średni wynik (lub mieć na myśli) jest sumą wszystkich wyników podzielonych przez dziewięć. To działa na 144/9 = 16. Zauważ, że chociaż 16 jest średnią arytmetyczną, jest zniekształcona przez niezwykle wysoki wynik 83 w porównaniu z innymi wynikami. Prawie wszystkie wyniki uczniów są poniżej Średnia. Dlatego w tym przypadku średnia nie jest dobrym przedstawicielem tendencji centralnej tej próbki.
mediana, Z drugiej strony jest wartością, która jest taka, że połowa wyników jest nad nią i połowa wyników poniżej. Więc w tym przykładzie mediana to 8. Istnieją cztery wyniki poniżej i cztery powyżej wartości 8. Więc 8 reprezentuje punkt środkowy lub centralną tendencję próbki.
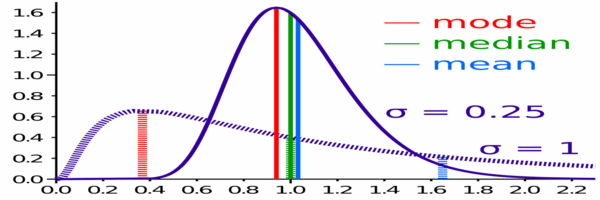Porównanie średniej, mediany i trybu dwóch logarytmicznych rozkładów o różnej skośności. Wady arytmetycznych środków i median
Średnia nie jest solidnym narzędziem statystycznym, ponieważ nie można go zastosować do wszystkich rozkładów, ale jest łatwo najczęściej używanym narzędziem statystycznym do uzyskania centralnej tendencji. Powodem, dla którego nie można zastosować do wszystkich rozkładów, jest to, że mają nadmierne wpływ na wartości w próbce, które są zbyt małe, aby zbyt duże.
Wadą mediany jest to, że trudno jest sobie z tym poradzić. Nie ma łatwego wzoru matematycznego do obliczenia mediany.
Inne rodzaje środków
Istnieje wiele sposobów określenia centralnej tendencji lub średniej zbioru wartości. Średnia omówiona powyżej jest technicznie średnią arytmetyczną i jest najczęściej stosowaną statystyką dla średniej. Istnieją inne rodzaje środków:
Średnia geometryczna
Średnia geometryczna jest zdefiniowana jako NKorzeń produktu N Liczby, ja.mi., dla zestawu liczb X1,X2,… ,XN, Średnia geometryczna jest zdefiniowana jako
Środki geometryczne są lepsze niż środki arytmetyczne do opisu proporcjonalnego wzrostu. Na przykład dobrym zastosowaniem dla średniej geometrycznej jest obliczanie złożonej rocznej tempa wzrostu (CAGR).
Średnia harmoniczna
Średnia harmoniczna jest wzajemną średnią arytmetyczną wzajemności. Średnia harmoniczna H pozytywnych liczb rzeczywistych X1,X2,… ,XN Jest
Dobrym zastosowaniem środków harmonicznych jest uśrednianie wielokrotności. W przypadku Exampe lepiej jest stosować średnią harmoniczną przy obliczaniu średniego stosunku ceny (P/E). Jeśli stosunki P/E są uśredniane za pomocą ważonej średniej arytmetyki, wysokie punkty danych są nadmiernie większe niż niskie punkty danych.
Pitagorean oznacza
Średnia arytmetyczna, średnia geometryczna i średnia harmoniczna razem tworzą zestaw średnich zwanych średnimi pitagoreanami. W przypadku dowolnego zestawu liczb średnia harmoniczna jest zawsze najmniejsza ze wszystkich środków Pitagoran, a średnia arytmetyczna jest zawsze największą z 3 średnich. I.mi. Średnia harmoniczna ≤ średnia geometryczna ≤ średnia arytmetyczna.
Inne znaczenia słów
Mieć na myśli może być używane jako postać mowy i ma literackie odniesienie. Służy również do sugerowania biednych lub nie jest świetnych. Mediana, W odniesieniu geometrycznym jest linia prosta przechodząca z punktu w trójkącie do środka przeciwnej strony.