Różnica między różnicowaniem a integracją

Rachunek jest jednym z podstawowych zastosowań matematycznych, które są obecnie stosowane na świecie do rozwiązania różnych zjawisk. Jest wysoce stosowany w badaniach naukowych, badaniach ekonomicznych, finansach i inżynierii między innymi dyscyplinami, które odgrywają istotną rolę w życiu jednostki. Integracja i różnicowanie to podstawy stosowane w rachunku różniczkowym do badania zmiany. Jednak wiele osób, w tym studentów i uczonych nie było w stanie podkreślić różnic między różnicowaniem a integracją.

Co to jest różnicowanie?

Różnicowanie jest terminem używanym w rachunku różniczym w odniesieniu do zmiany, które właściwości doświadczają dotyczące zmiany jednostki w innej powiązanej właściwości.

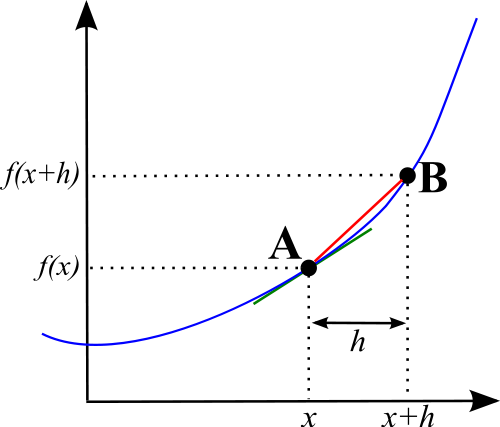
W innym terminie różnicowanie tworzy wyrażenie algebraiczne, które pomaga w obliczeniach gradient krzywej w danym punkcie. Ważne jest, aby podkreślić, że krzywe mają swoje nachylenia w danym punkcie, w przeciwieństwie do linii prostych, które mają ten sam gradient przez cały czas.

Co to jest integracja?

Integracja jest terminem stosowanym w rachunku różniczym w odniesieniu do wzoru i procedury obliczania obszaru pod krzywą.

Warto zauważyć, że wykres musi znajdować się pod krzywą, co wynika z tworzenia części integralnej, co jest trudne do znalezienia obszaru w przeciwieństwie do innych kształtów, takich jak koła, kwadraty i prostokąty, które są łatwiejsze do obliczenia ich obszarów.

Różnica między różnicowaniem a integracją

1) Cel i funkcje różnicowania i integracji

Integracja i różnicowanie można przede wszystkim zróżnicować w sposobie stosowania dwóch koncepcji i ich ostatecznych wyników. Są używane do osiągnięcia różnych odpowiedzi, co jest podstawową różnicą. Zróżnicowanie stosuje się do obliczania gradientu krzywej. Krzywe nieliniowe mają różne zbocza w dowolnym punkcie, co utrudnia określenie ich gradientów. Wyrażenie algebraiczne zastosowane do określenia zmiany poniesionej od jednego punktu do drugiego z jednostką jest określane jako różnicowanie.  Z drugiej strony integracja jest wyrażeniem algebraicznym stosowanym do obliczania obszaru pod krzywą, ponieważ nie jest idealnym kształtem, po którym można łatwo obliczyć obszar.

2) bezpośrednio naprzeciwko

Funkcje algebraiczne różnicowania i integracji są bezpośrednio przeciwne do siebie, szczególnie w ich zastosowaniu. Jeśli ktoś wykonuje integrację, mówi się, że pokazuje przeciwieństwo różnicowania, podczas gdy jeśli ktoś wykonuje różnicowanie, wykonuje przeciwieństwo integracji. Na przykład integracja i różnicowanie tworzą relację, która jest podobnie przedstawiona, gdy wykonuje się kwadrat liczby, a następnie znajduje pierwiastek kwadratowy wyniku. Dlatego jeśli ktoś chce znaleźć przeciwieństwo zintegrowanej liczby, będzie zobowiązany do wykonania zróżnicowania tej samej liczby. Po prostu integracja jest odwrotnym procesem różnicowania i odwrotnie.

3) Zastosowanie prawdziwego życia do różnicowania i integracji

W rzeczywistych scenariuszach stwierdzono, że integracja i różnicowanie są stosowane inaczej niż każda koncepcja zastosowana w zapewnianiu różnych wyników. Niemniej jednak niezwykłe jest podkreślenie, że oba różnicowanie są niezbędnymi koncepcjami rachunku różniczkowego, które ułatwiają życie. Jednym z głównych zastosowań integracji jest obliczenie obszarów zakrzywionych powierzchni, obliczanie objętości obiektów i obliczanie centralnego punktu między innymi.

Z drugiej strony koncepcja różnicowania jest istotnie stosowana do obliczania prędkości chwilowej i stosowana w ustalaniu, czy funkcja rośnie, czy odpowiednio się zmniejsza. Jest to wyraźna demonstracja tego, w jaki sposób te dwie koncepcje są stosowane w życiu jednostek.

4) Szybkość i funkcja różnicowania i integracji

Inną różnicą między integracją a różnicowaniem jest rola, jaką odgrywają, jeśli chodzi o każdą badaną funkcję. Według matematyków różnicowanie znacznie pomaga w określaniu prędkości funkcji, pomagając w obliczaniu prędkości chwilowej. Z drugiej strony integracja dotyczy określania dystansowanej podróży przez dowolną funkcję. Obszar pod krzywą szacuje się na równoważność odległości przebywającej przez funkcję. Ekspresja algebraiczna integracji pomaga w obliczeniu obszaru pod krzywą, co stanowi odległość przebywającą przez funkcję.

Wyrażenia algebraiczne/wzór do różnicowania i integracji

Warto również zauważyć, że różnicowanie i integracja mają różne wyrażenia algebraiczne, które są używane w obliczeniach. To wyjaśnia, dlaczego dwie koncepcje rachunku różniczkowego zawsze zapewnią różne wyniki.  Pochodna funkcji f (x) dotycząca zmiennej x i zgodnie z regułą produktu zostanie zdefiniowana jako:

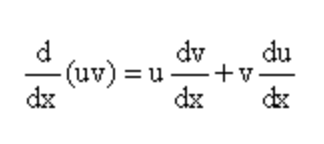
Z drugiej strony formuła integracji lub obszar całki pod krzywą można obliczyć za pomocą wzoru:

∫f (x) dx, która jest formułem przyjętą w metodzie zastępczej.

5) Dodanie i podział

Inną metodą porównywania integracji z różnicowaniem jest specyficzne wyjaśnienie, w jaki sposób każda funkcja realizuje jej wyniki. Integracja określa wynik określonej funkcji poprzez dodanie aspektów związanych z obliczeniami. Z drugiej strony różnicowanie określa szybkość natychmiastową i prędkość funkcji poprzez podział.

Różnice między różnicowaniem a integracją: wykres porównawczy

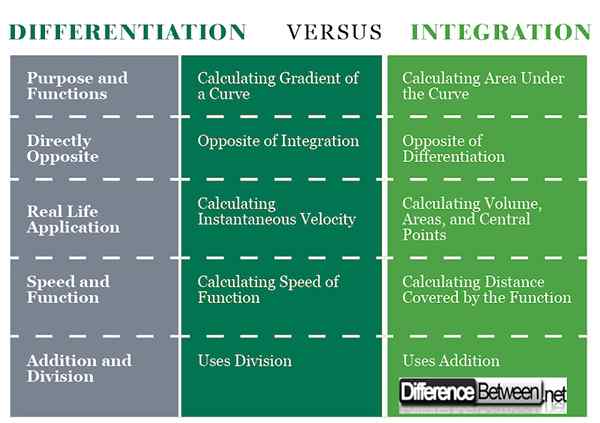
Podsumowanie różnicowania vs. Integracja

• Jedną z głównych zmian między różnicowaniem a integracją jest to, że dwie funkcje rachunku różniczkowego są bezpośrednio przeciwne do siebie w ich zastosowaniu.
• Uczniowie i inni uczeni powinni skupić się na zrozumieniu jednej z pojęć, po których będą musieli wykonać odwrotnie, aby określić wyniki drugiej funkcji.
• Zrozumienie różnic między integracją a różnicowaniem jest niezbędne, ponieważ pomoże osobom w użyciu właściwej ekspresji algebraicznej w razie potrzeby.
• Wreszcie, ważne jest opanowanie dwóch koncepcji rachunku w podstawowej matematyce, ponieważ były one konsekwentnie używane w różnych dyscyplinach, takich jak ekonomia, biznes i inżynieria.