Różnica między integralami określonymi i nieokreślonymi
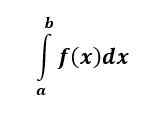
- 2207
- 452
- Prokop Cebula
Rachunek jest ważną gałęzią matematyki, a różnicowanie odgrywa kluczową rolę w rachunku rachunkowym. Odwrotny proces różnicowania jest znany jako integracja, a odwrotność jest znana jako całka lub po prostu, odwrotność różnicowania daje całkę. Na podstawie wyników wytwarzają całki są podzielone na dwie klasy, a mianowicie., określone i nieokreślone całki.
Określona całka
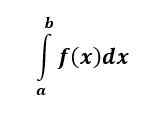
Określona całka f (x) jest liczbą i reprezentuje obszar pod krzywą f (x) z x = a Do x = b.
Zdecydowana całka ma górne i dolne limity całek i nazywa się ją określonymi, ponieważ na końcu problemu mamy liczbę - jest to zdecydowana odpowiedź.
Integral nieokreślony
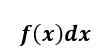
Nieokreślona całka F (x) jest funkcją i odpowiada na pytanie: „Jaką funkcję, gdy daje zróżnicowana f (x)?"
Z nieokreśloną całką nie ma tutaj górnych i dolnych limitów całki, a to, co otrzymamy, to odpowiedź, która wciąż ma Xjest w nim i będzie miał stałą (zwykle oznaczoną przez C) w tym.
Integra nieokreślona zwykle daje ogólne rozwiązanie równania różniczkowego.
Integra nieokreślona jest bardziej ogólną formą integracji i można ją interpretować jako anty-pochodząca z rozważanej funkcji.
Załóżmy, że zróżnicowanie funkcji F prowadzi do innej funkcji F, a integracja F daje całkę. Symbolicznie, jest to napisane jako
F (x) = ∫ƒ (x) dx
Lub
F = ∫ƒ dx
gdzie oba F I ƒ są funkcjami X, I F jest różnicowy. W powyższej formie nazywa się to całka Reimanna, a wynikowa funkcja towarzyszy dowolnej stałej.
Nieokreślona całka często wytwarza rodzinę funkcji; Dlatego całka jest nieokreślona.
Integrale i proces integracji leżą u podstaw rozwiązywania równań różniczkowych. Jednak w przeciwieństwie do etapów różnicowania, kroki w integracji nie zawsze są zgodne z wyraźną i standardową rutyną. Czasami widzimy, że rozwiązania nie można wyraźnie wyrazić w kategoriach funkcji elementarnej. W takim przypadku rozwiązanie analityczne jest często podawane w postaci całki nieokreślonej.
Podstawowe twierdzenie rachunku różniczkowego
Zdecydowana i nieokreślona całka jest powiązana z podstawowym twierdzeniem rachunku różniczkowego w następujący sposób: w celu obliczenia a określona całka, znaleźć Integral nieokreślony (znany również jako anty-pochodząca) funkcji i ocena w punktach końcowych x = a I x = b.
Różnica między integralami określonymi i nieokreślonymi będzie widoczna po oceny całek dla tej samej funkcji.
Rozważ następującą całkę:
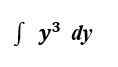
OK. Zróbmy ich oboje i zobaczmy różnicę.
W celu integracji musimy dodać jeden do indeksu, który prowadzi nas do następującego wyrażenia:
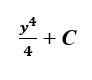
W tym momencie C jest dla nas jedynie stałym. Potrzebne są dodatkowe informacje, aby określić dokładną wartość C.
Oceńmy tę samą całkę w jego określonej formie I.mi., z uwzględnieniem górnych i dolnych limitów.
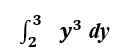
Graficznie, obliczamy teraz obszar pod krzywą f (x) = y3 między y = 2 I y = 3.
Pierwszy krok w tej ocenie jest taki sam, jak nieokreślona ocena integralna. Jedyną różnicą jest to, że tym razem nie dodajemy stałej C.
Wyrażenie w tym przypadku wygląda następująco:
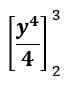
To jest zwrot do:
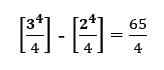
Zasadniczo zastąpiliśmy 3, a następnie 2 w wyrażeniu i uzyskaliśmy różnicę między nimi.
Jest to określona wartość, w przeciwieństwie do używania stałego C wcześniej.
Zbadajmy stały czynnik (w odniesieniu do całki nieokreślonej) w bardziej szczegółowych szczegółach.
Jeśli różnica y3 Jest 3y2, Następnie
∫3y2dy = y3
Jednakże, 3y2 może być różnicą wielu wyrażeń, z których niektóre z nich obejmują y3-5, y3+7, itp.… To oznacza, że odwrócenie nie jest unikalne, ponieważ stała nie jest uwzględniona podczas operacji.
Tak ogólnie, 3y2 jest różnicą y3+C Gdzie C jest każda stała. Nawiasem mówiąc, C jest znany jako „Stała integracji”.
Piszemy to jako:
∫ 3y2.dx = y3 + C
Techniki integracji dla nieokreślonej całki, takie jak wyszukiwanie tabeli lub integracja RISCH, mogą dodać nowe nieciągłości podczas procesu integracji. Te nowe nieciągłości pojawiają się, ponieważ anty-pochodzenie mogą wymagać wprowadzenia złożonych logarytmów.
Złożone logarytmy mają nieciągłość skoku, gdy argument przekroczy negatywną oś rzeczywistą, a algorytmy integracji czasami nie mogą znaleźć reprezentacji, w której skoki te anulują.
Jeśli określona całka jest oceniana przez najpierw obliczenie całki nieokreślonej, a następnie zastąpienie granic integracji w wyniku, musimy pamiętać, że integracja nieokreślona może powodować nieciągłości. Jeśli tak się stanie, musimy zbadać nieciągłości w przedziale integracji.

