Różnica między korelacją a regresją
- 4680
- 1123
- Patrycy Ziółkowski
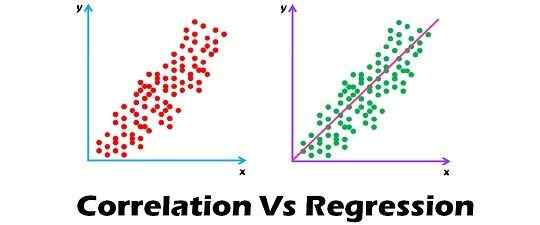
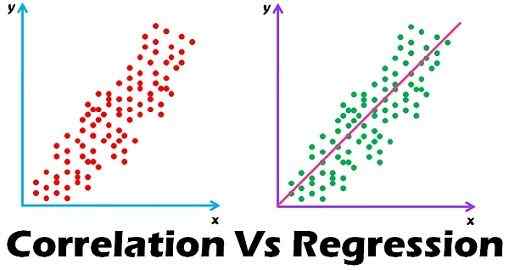 Korelacja i regresja to dwie analizy oparte na rozkładowi wielowymiarowym. Rozkład wielowymiarowy jest opisany jako rozkład wielu zmiennych. Korelacja jest opisywany jako analiza, która pozwala nam poznać powiązanie lub brak związku między dwiema zmiennymi „x” i „y”. Na drugim końcu, Regresja Analiza przewiduje wartość zmiennej zależnej na podstawie znanej wartości zmiennej niezależnej, zakładając, że średnia zależność matematyczna między dwiema lub więcej zmiennymi.
Korelacja i regresja to dwie analizy oparte na rozkładowi wielowymiarowym. Rozkład wielowymiarowy jest opisany jako rozkład wielu zmiennych. Korelacja jest opisywany jako analiza, która pozwala nam poznać powiązanie lub brak związku między dwiema zmiennymi „x” i „y”. Na drugim końcu, Regresja Analiza przewiduje wartość zmiennej zależnej na podstawie znanej wartości zmiennej niezależnej, zakładając, że średnia zależność matematyczna między dwiema lub więcej zmiennymi.
Różnica między korelacją a regresją jest jednym z powszechnie zadawanych pytań w wywiadach. Ponadto wiele osób cierpi z dwuznaczności w zrozumieniu tych dwóch. Więc przeczytaj pełny artykuł, aby mieć jasne zrozumienie tych dwóch.
Treść: korelacja a regresja
- Wykres porównania
- Definicja
- Kluczowe różnice
- Wideo
- Wniosek
Wykres porównania
| Podstawa do porównania | Korelacja | Regresja |
|---|---|---|
| Oznaczający | Korelacja jest miarą statystyczną, która określa współrenację lub powiązanie dwóch zmiennych. | Regresja opisuje, w jaki sposób zmienna niezależna jest numerycznie powiązana ze zmienną zależną. |
| Stosowanie | Reprezentować liniową zależność między dwiema zmiennymi. | Aby dopasować najlepszą linię i oszacować jedną zmienną na podstawie innej zmiennej. |
| Zmienne zależne i niezależne | Bez różnicy | Obie zmienne są różne. |
| Wskazuje | Współczynnik korelacji wskazuje stopień, w jakim dwie zmienne poruszają się razem. | Regresja wskazuje wpływ zmiany jednostki w znanej zmiennej (x) na szacowaną zmienną (y). |
| Cel | Znaleźć wartość numeryczną wyrażającą związek między zmiennymi. | Aby oszacować wartości zmiennej losowej na podstawie wartości zmiennej stałej. |
Definicja korelacji
Termin korelacja jest kombinacją dwóch słów „CO” (razem) i relacji (połączenia) między dwiema wielkościami. Korelacja ma miejsce, gdy w momencie badania dwóch zmiennych obserwuje się, że zmiana jednostkowa jednej zmiennej jest odwetowana przez równoważną zmianę w innej zmiennej, i.mi. bezpośredni lub pośredni. Albo mówi się, że zmienne są nieskorelowane, gdy ruch w jednej zmiennej nie oznacza żadnego ruchu w innej zmiennej w określonym kierunku. Jest to technika statystyczna, która reprezentuje siłę połączenia między parami zmiennych.
Korelacja może być pozytywna lub ujemna. Kiedy dwie zmienne poruszają się w tym samym kierunku, ja.mi. Wzrost jednej zmiennej spowoduje odpowiedni wzrost innej zmiennej i odwrotnie, wówczas zmienne są uważane za dodatnio skorelowane. Na przykład: Zysk i inwestycje.
Przeciwnie, gdy dwie zmienne poruszają się w różnych kierunkach, w taki sposób, że wzrost jednej zmiennej spowoduje zmniejszenie innej zmiennej i odwrotnie, sytuacja ta jest znana jako korelacja ujemna. Na przykład: Cena i popyt na produkt.
Miary korelacji podano jako poniżej:
- Współczynnik korelacji produktu Karla Pearsona
- Współczynnik korelacji rangi Spearmana
- Schemat rozproszenia
- Współczynnik współbieżnych odchyleń
Definicja regresji
Technika statystyczna do oszacowania zmiany zmiennej zależnej od metryki ze względu na zmianę jednej lub więcej zmiennych niezależnych, w oparciu o średnią zależność matematyczną między dwiema lub więcej zmiennymi, jest znana jako regresja. Odgrywa znaczącą rolę w wielu działalności człowieka, ponieważ jest to potężne i elastyczne narzędzie, które wykorzystywało się do prognozowania przeszłych, obecnych lub przyszłych wydarzeń na podstawie przeszłych lub obecnych wydarzeń. Na przykład: Na podstawie wcześniejszych rekordów można oszacować przyszły zysk firmy.
W prostej regresji liniowej istnieją dwie zmienne x i y, w których y zależy od x lub powiedz, że wpływa x. Tutaj y jest nazywane jako zmienna zależna lub kryterium, a x jest niezależna lub zmienna predykcyjna. Linia regresji y na x jest wyrażona jako poniżej:
y = a + bx
gdzie, a = stała,
B = współczynnik regresji,
W tym równaniu A i B są dwoma parametrami regresji.
Kluczowe różnice między korelacją a regresją
Punkty podane poniżej, szczegółowo wyjaśnia różnicę między korelacją a regresją:
- Miara statystyczna, która określa wspólne relację lub powiązanie dwóch ilości, jest znana jako korelacja. Regresja opisuje, w jaki sposób zmienna niezależna jest numerycznie powiązana ze zmienną zależną.
- Korelacja służy do przedstawienia liniowej zależności między dwiema zmiennymi. Przeciwnie, regresja służy do dopasowania najlepszej linii i oszacowania jednej zmiennej na podstawie innej zmiennej.
- W korelacji nie ma różnicy między zmiennymi zależnymi i niezależnymi i.mi. korelacja między x i y jest podobna do y i x. I odwrotnie, regresja y na x różni się od x na y.
- Korelacja wskazuje na siłę związku między zmiennymi. W przeciwieństwie do regresji odzwierciedla wpływ zmiany jednostki w zmiennej niezależnej na zmienną zależną.
- Korelacja ma na celu znalezienie wartości numerycznej, która wyraża związek między zmiennymi. W przeciwieństwie do regresji, której celem jest przewidywanie wartości zmiennej losowej na podstawie wartości zmiennej stałej.
Wideo: korelacja a regresja
Wniosek
W powyższej dyskusji jest oczywiste, że istnieje duża różnica między tymi dwoma koncepcjami matematycznymi, chociaż te dwa są badane razem. Korelacja jest stosowana, gdy badacz chce wiedzieć, czy badane zmienne są skorelowane, czy nie, to jaka jest siła ich powiązania. Współczynnik korelacji Pearsona jest uważany za najlepszą miarę korelacji. W analizie regresji ustalono funkcjonalny związek między dwiema zmiennymi, aby dokonać przyszłych prognoz zdarzeń.
- « Różnica między wspólnym przedsięwzięciem a sojuszem strategicznym
- Różnica między oceną formatywną i podsumowującą »

