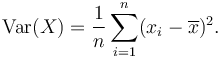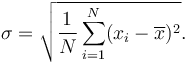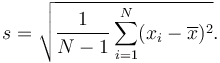Odchylenie standardowe vs. Zmienność

- 3930
- 95
- Marta Ruciński
Odchylenie standardowe I zmienność to statystyczne miary dyspersji danych, i.mi., Reprezentują, ile jest zmienności ze średniej lub w jakim stopniu wartości zwykle „odbiegają” od średniej (średnia). Wariancja lub odchylenie standardowe zero wskazuje, że wszystkie wartości są identyczne.
Wariancja jest średnią kwadratów odchyleń (i.mi., Różnica w wartościach od średniej), a odchylenie standardowe jest pierwiastkiem kwadratowym tej wariancji. Odchylenie standardowe służy do identyfikacji wartości odstających w danych.
Wykres porównania
Różnice - podobieństwa -| Odchylenie standardowe | Zmienność | |
|---|---|---|
| Matematyczna formuła | Pierwiastek kwadratowy wariancji | Średnia kwadratów odchyleń każdej wartości od średniej w próbce. |
| Symbol | Grecka litera sigma - σ | Brak dedykowanego symbolu; wyrażone w kategoriach odchylenia standardowego lub innych wartości. |
| Wartości w odniesieniu do podanego zestawu danych | Ta sama skala co wartości w danym zestawie danych; Dlatego wyrażone w tych samych jednostkach. | Skala większa niż wartości w danym zestawie danych; nie wyrażone w tej samej jednostce co same wartości. |
| Czy wartości są ujemne lub dodatnie? | Zawsze nie wymagające | Zawsze nie wymagające |
| Aplikacja w świecie rzeczywistym | Pobieranie próbek populacji; identyfikacja wartości odstających | Formuły statystyczne, finanse. |
Ważne pojęcia
- Mieć na myśli: Średnia wszystkich wartości w zestawie danych (dodaj wszystkie wartości i podziel ich sumę przez liczbę wartości).
- Odchylenie: odległość każdej wartości od średniej. Jeśli średnia wynosi 3, wartość 5 ma odchylenie 2 (odejmij średnią od wartości). Odchylenie może być pozytywne lub negatywne.
Symbolika
Wzór odchylenia standardowego i wariancji jest często wyrażany przy użyciu:
- x̅ = średnia lub średnia wszystkich punktów danych w problemie
- X = indywidualny punkt danych
- N = liczba punktów w zestawie danych
- ∑ = suma [kwadratów odchyleń]
Formuły
Wariancja zestawu N Równie prawdopodobne wartości można zapisać jako:
Odchylenie standardowe jest pierwiastkiem kwadratowym wariancji:
Formuły z greckim literami mają sposób na zniechęcając, ale to mniej skomplikowane, niż się wydaje. Aby umieścić to w prostych krokach:
- Znajdź średnią wszystkich punktów danych
- Dowiedz się, jak daleko każdy punkt jest z dala od średniej (to jest odchylenie)
- kwadratowe każde odchylenie (i.mi. różnica każdej wartości ze średniej)
- podziel sumę kwadratów przez liczbę punktów.
To daje wariancję. Weź pierwiastek kwadratowy wariancji, aby znaleźć odchylenie standardowe.
Ten doskonały film z Khan Academy wyjaśnia pojęcia wariancji i odchylenia standardowego:
Przykład
Powiedzmy, że zestaw danych zawiera wysokość sześciu mniszek lekarskich: 3 cale, 4 cale, 5 cali, 4 cale, 11 cali i 6 cali.
Najpierw znajdź średnią punktów danych: (3 + 4 + 5 + 4 + 11 + 7) / 6 = 5.5
Więc średnia wysokość wynosi 5.5 cali. Teraz potrzebujemy odchyleń, więc znajdujemy różnicę każdej rośliny od średniej: -2.5, -1.5, -.5, -1.5, 5.5, 1.5
Teraz kwadrat każde odchylenie i znajdź ich sumę: 6.25 + 2.25 + .25 + 2.25 + 30.25 + 2.25 = 43.5
Teraz podziel sumę kwadratów przez liczbę punktów danych, w tym przypadku rośliny: 43.5 /6 = 7.25
Więc wariancja tego zestawu danych wynosi 7.25, co jest dość dowolną liczbą. Aby przekonwertować go w rzeczywisty pomiar, weź pierwiastek kwadratowy 7.25 Aby znaleźć odchylenie standardowe w calach.
Odchylenie standardowe wynosi około 2.69 cali. Oznacza to, że dla próbki każdy mnóstwo w ciągu 2.69 cali średniej (5.5 cali) jest „normalne”.
Dlaczego kwadratowe odchylenia?
Odchylenia są kwadratowe, aby zapobiec wartościom ujemnym (odchylenia poniżej średniej) odwołania wartości dodatnich. Działa to, ponieważ liczba ujemna kwadrat staje się wartością dodatnią. Jeśli miałeś prosty zestaw danych z odchyleniami od średniej +5, +2, -1 i -6, suma odchyleń wyjdzie jako zero, jeśli wartości nie są kwadratowe (i.mi. 5 + 2 - 1 - 6 = 0).
Aplikacje w świecie rzeczywistym
Wariancja jest wyrażona jako dyspersja matematyczna. Ponieważ jest to dowolna liczba w stosunku do oryginalnych pomiarów zestawu danych, trudno jest wizualizować i zastosować w sensie rzeczywistym. Znalezienie wariancji jest zwykle ostatnim krokiem przed znalezieniem odchylenia standardowego. Wartości wariancji są czasami stosowane w formułach finansowych i statystycznych.
Odchylenie standardowe, które jest wyrażone w oryginalnych jednostkach zestawu danych, jest znacznie bardziej intuicyjne i bliższe wartości oryginalnego zestawu danych. Najczęściej stosuje się go do analizy demografii lub próbek populacji, aby uzyskać poczucie tego, co jest normalne w populacji.
Znajdowanie wartości odstających
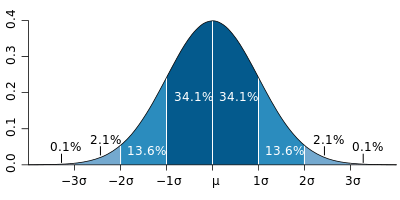 Rozkład normalny (krzywa dzwonowa) z pasmami odpowiadającymi 1σ
Rozkład normalny (krzywa dzwonowa) z pasmami odpowiadającymi 1σ W rozkładowi normalnym około 68% populacji (lub wartości) należy do 1 odchylenia standardowego (1σ) średniej, a około 94% mieści się w 2σ. Wartości, które różnią się od średniej przez 1.7σ lub więcej są zwykle uważane za wartości odstające.
W praktyce systemy jakości, takie jak Six Sigma, próbują zmniejszyć szybkość błędów, aby błędy stały się odstające. Termin „proces Six Sigma” wynika z poglądu, że jeśli ktoś ma sześć standardowych odchyleń między średnią procesu a najbliższym limitem specyfikacji, praktycznie żadne elementy nie spełni specyfikacji.[1]
Odchylenie standardowe próbki
W aplikacjach w świecie rzeczywistym używane zestawy danych zwykle reprezentują próbki populacji, a nie całe populacje. Nieco zmodyfikowana formuła stosuje się, jeśli należy wyciągnąć wnioski całej populacji z częściowej próbki.
„Odchylenie standardowe” jest używane, jeśli wszystko, co masz
Jedynym sposobem, w jaki wzór odchylenia standardowego próbki różni się od wzoru odchylenia standardowego, jest „-1” w mianowniku.
Korzystając z przykładu mniszka lekarskiego, ten wzór byłby potrzebny, gdybyśmy pobrali próbki tylko 6 mniszek lekarskich, ale chcieli użyć tej próbki do podania odchylenia standardowego dla całego pola z setkami mniszek leków.
Suma kwadratów byłaby teraz podzielona przez 5 zamiast 6 (n - 1), co daje wariancję 8.7 (zamiast 7.25) i przykładowe odchylenie standardowe 2.95 cali, zamiast 2.69 cali dla oryginalnego odchylenia standardowego. Ta zmiana służy do znalezienia marginesu błędu w próbce (9% w tym przypadku).