Różnica między testem t i testem Z

- 3344
- 803
- Hilarion Porębski
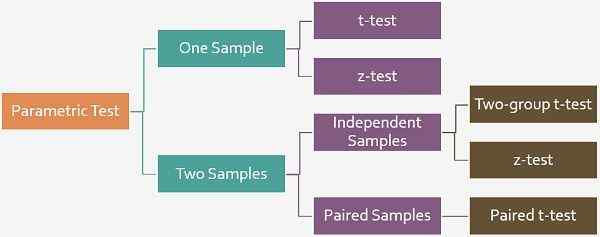 Test t odnosi się do testu hipotezy jednoczynnikowej opartej na statystyce T, w której średnia jest znana, a wariancja populacji jest aproksymowana z próbki. Z drugiej strony, Test Z jest również testem jednoczynnikowym opartym na standardowym rozkładowi normalnym.
Test t odnosi się do testu hipotezy jednoczynnikowej opartej na statystyce T, w której średnia jest znana, a wariancja populacji jest aproksymowana z próbki. Z drugiej strony, Test Z jest również testem jednoczynnikowym opartym na standardowym rozkładowi normalnym.
Mówiąc prosto, hipoteza odnosi się do przypuszczenia, które ma zostać zaakceptowane lub odrzucone. Istnieją dwie procedury testowania hipotez, i.mi. Test parametryczny i test nieparametryczny, w którym test parametryczny opiera się na fakcie, że zmienne są mierzone w skali przedziału, podczas gdy w teście nieParametrycznym jest to samo mierzone w skali porządkowej. Teraz, w teście parametrycznym, mogą istnieć dwa rodzaje testu, test t i test Z.
W tym artykule szczegółowo zrozumiesz różnicę między testem t a testem Z.
Treść: Test t vs-Z-test
- Wykres porównania
- Definicja
- Kluczowe różnice
- Wniosek
Wykres porównania
| Podstawa do porównania | Test t | Test Z |
|---|---|---|
| Oznaczający | Test t odnosi się do rodzaju testu parametrycznego, który jest stosowany do identyfikacji, w jaki sposób środki dwóch zestawów danych różnią się od siebie, gdy wariancja nie jest podana. | Z-testu oznacza test hipotezy, który ustalenia, czy środki dwóch zestawów danych różnią się od siebie, gdy podaje się wariancję. |
| Oparte na | Dystrybucja studenta-T | Normalna dystrybucja |
| Wariancja populacji | Nieznany | Znany |
| Wielkość próbki | Mały | Duży |
Definicja testu t
Test t to test hipotezy zastosowany przez naukowca w celu porównania średnich populacji dla zmiennej, sklasyfikowanych do dwóch kategorii w zależności od mniejszej niż zmiennej interwałowej. Mówiąc dokładniej, test T jest używany do zbadania, w jaki sposób różnią się środki pobrane z dwóch niezależnych próbek.
Test t następuje po dystrybucji T, co jest odpowiednie, gdy wielkość próby jest niewielka, a odchylenie standardowe populacji nie jest znane. Na kształt dystrybucji T jest wysoce wpływ na stopień wolności. Stopień swobody implikuje liczbę niezależnych obserwacji w danym zestawie obserwacji.
Założenia testu t:
- Wszystkie punkty danych są niezależne.
- Rozmiar próbki jest mały. Zasadniczo wielkość próby przekraczająca 30 jednostek próbek jest uważana za duże, w przeciwnym razie niewielkie, ale nie powinno to być mniejsze niż 5, aby zastosować test t.
- Wartości przykładowe należy dokładnie przyjmować i rejestrować.
Statystyka testowa to:
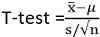
x ̅ Czy średnia próbki
S to odchylenie standardowe próbki
n to wielkość próbki
μ jest średnią populacji
Sparowany test t: Test statystyczny zastosowano, gdy dwie próbki są zależne i pobierane są sparowane obserwacje.
Definicja testu Z
Test Z odnosi się do jednoczynnikowej analizy statystycznej zastosowanej do przetestowania hipotezy, że proporcje dwóch niezależnych próbek różnią się znacznie. Określa, w jakim stopniu punkt danych jest z dala od średniej zbioru danych, w odchyleniu standardowym.
Badacz przyjmuje test Z, gdy wariancja populacji jest znana w zasadzie, gdy istnieje duża wielkość próby, wariancja próbki uważa się za w przybliżeniu równą wariancji populacji. W ten sposób zakłada się, że jest znany, pomimo faktu, że dostępne są tylko dane próbki, a więc można zastosować normalny test.
Założenia testu Z:
- Wszystkie obserwacje przykładowe są niezależne
- Rozmiar próbki powinien wynosić więcej niż 30.
- Rozkład Z jest normalny, ze średnią zero i wariancją 1.
Statystyka testowa to:
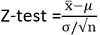
x ̅ Czy średnia próbki
σ to odchylenie standardowe populacji
n to wielkość próbki
μ jest średnią populacji
Kluczowe różnice między testem t i testem Z
Różnica między testem t a testem Z można wyraźnie wyciągnąć na następujących podstawach:
- Test t można rozumieć jako test statystyczny, który służy do porównania i analizy, czy środki tej dwóch populacji są różne od siebie, czy nie, gdy odchylenie standardowe nie jest znane. W porównaniu z testem Z jest testem parametrycznym, który jest stosowany, gdy znany jest odchylenie standardowe, aby ustalić, czy środki z dwóch zestawów danych różnią się od siebie.
- Test t oparty na dystrybucji studenta. Przeciwnie, test Z opiera się na założeniu, że rozkład średnich próbek jest normalny. Zarówno dystrybucja studenta, jak i rozkład normalny wydają się podobne, ponieważ oba są symetryczne i w kształcie dzwonu. Różnią się jednak w tym sensie, że w dystrybucji T jest mniej miejsca na środku i więcej w ogonach.
- Jednym z ważnych warunków przyjęcia testu T jest to, że wariancja populacji jest nieznana. I odwrotnie, wariancja populacji należy znać lub zakładać, że jest znana w przypadku testu Z.
- Test Z jest używany do gdy wielkość próbki jest duża, i.mi. n> 30, a test t jest odpowiedni, gdy rozmiar próbki jest mały, w tym sensie < 30.
Wniosek
Ogólnie rzecz biorąc, test t i test Z są prawie podobnymi testami, ale warunki ich zastosowania są różne, co oznacza, że test t jest odpowiedni, gdy rozmiar próbki wynosi nie więcej niż 30 jednostek. Jeśli jednak jest to więcej niż 30 jednostek, należy wykonać test Z. Podobnie istnieją inne warunki, które wyjaśniają, który test ma być wykonany w danej sytuacji.
- « Różnica między ubezpieczeniem pożarowym a ubezpieczeniem morskim
- Różnica między audytem a recenzją »

