Różnica między średnią próbką a średnią populacji

- 4623
- 293
- Łukasz Kalisz
 W statystykach średnia arytmetyczna jest jednym z idealnych miar tendencji centralnej. Dla danego zestawu obserwacji średnia arytmetyczna można obliczyć, dodając wszystkie obserwacje i dzieląc wartość uzyskaną przez liczbę obserwacji. Istnieją dwa rodzaje średniej, i.mi. Średnia próbki i średnia populacji, która jest często stosowana w statystykach i prawdopodobieństwie. Średnia próbki jest wykorzystywana głównie do oszacowania średniej populacji, gdy średnia populacji nie jest znana, ponieważ mają one taką samą wartość oczekiwaną.
W statystykach średnia arytmetyczna jest jednym z idealnych miar tendencji centralnej. Dla danego zestawu obserwacji średnia arytmetyczna można obliczyć, dodając wszystkie obserwacje i dzieląc wartość uzyskaną przez liczbę obserwacji. Istnieją dwa rodzaje średniej, i.mi. Średnia próbki i średnia populacji, która jest często stosowana w statystykach i prawdopodobieństwie. Średnia próbki jest wykorzystywana głównie do oszacowania średniej populacji, gdy średnia populacji nie jest znana, ponieważ mają one taką samą wartość oczekiwaną.
Średnia próbka implikuje średnią próbkę pochodzącą z całej populacji losowo. Populacja średnia to nic innego jak średnia z całej grupy. Rzuć okiem na ten artykuł, aby poznać różnice między średnią próbką a średnią populacji.
Treść: średnia próbki vs populacja średnia
- Wykres porównania
- Definicja
- Kluczowe różnice
- Wniosek
Wykres porównania
| Podstawa do porównania | Średnia próbka | Populacja średnia |
|---|---|---|
| Oznaczający | Średnia próbki jest średnią arytmetyczną losowych wartości próbki wyciągniętej z populacji. | Średnia populacji reprezentuje faktyczną średnią całej populacji. |
| Symbol | X̄ (wymawiane jako X) | μ (grecki termin MU) |
| Obliczenie | Łatwy | Trudny |
| Dokładność | Niski | Wysoki |
| Odchylenie standardowe | Po obliczeniu przy użyciu średniej próbki jest oznaczone przez (s). | Po obliczeniu przy użyciu średniej populacji jest oznaczone przez (σ). |
Definicja średniej próbki
Średnia próbki jest średnią obliczoną na podstawie grupy zmiennych losowych, wyciągniętej z populacji. Jest uważany za wydajny i obiektywny estymator populacji, co oznacza, że najbardziej oczekiwaną wartością dla statystyki próbki jest statystyka populacji, niezależnie od błędu próbkowania. Średnia próbki jest obliczana jako poniżej:
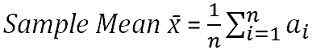 gdzie, n = rozmiar próbki
gdzie, n = rozmiar próbki
∑ = Sump Up
AI = Wszystkie obserwacje
Definicja populacji średniej
W statystykach średnia populacji jest definiowana jako średnia wszystkich elementów w populacji. Jest to średnia charakterystyczna grupy, w której grupa odnosi się do elementów populacji, takich jak przedmioty, osoby itp. a cecha jest przedmiotem zainteresowania. Ponieważ populacja jest bardzo duża i nie znana, średnia populacji jest nieznana stała. Za pomocą następującego wzoru można obliczyć średnią populacji,
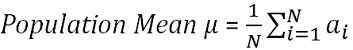 gdzie n = wielkość populacji
gdzie n = wielkość populacji
∑ = Sump Up
AI = Wszystkie obserwacje
Kluczowe różnice między średnią próbką a średnią populacji
Istotne różnice między średnią próbką a średnią populacji są szczegółowo wyjaśnione w punktach podanych poniżej:
- Średnia arytmetyczna losowych wartości próbki wyciągniętej z populacji nazywa się średnią próbką. Średnia arytmetyczna całej populacji nazywa się populacją.
- Próbka jest reprezentowana przez X̄ (wymawiane jako pasek X). Z drugiej strony średnia populacji jest oznaczona jako μ (grecki termin MU).
- Chociaż obliczenia średniej próbki jest łatwe, ponieważ lista dostarczonych elementów to tylko nieliczne, co zużywa bardzo mniej czasu. W przeciwieństwie do populacji, w których obliczenia są trudne, ponieważ istnieje wiele elementów w populacji, które zajmują dużo czasu.
- Dokładność średniej populacji jest stosunkowo wyższa niż średnia próbki. Dokładność średniej próbki można zwiększyć poprzez zwiększenie liczby obserwacji.
- Elementy populacji są reprezentowane przez „n” w populacji. Przeciwnie, „n” w średniej próbki reprezentuje wielkość próbki.
- Gdy odchylenie standardowe jest obliczane za pomocą średniej próbki, jest to oznaczone literą „s”. I odwrotnie, gdy średnia populacji jest stosowana w obliczaniu odchylenia standardowego, jest ona reprezentowana przez Sigma (σ).
Wniosek
Metoda obliczania obu średnich jest sama, i.mi. suma wszystkich obserwacji podzielonych przez liczbę obserwacji, ale istnieje duża różnica między tym, jak są reprezentowane. Podczas gdy średnia próbki jest zapisywana jako X̄ lub czasami M, średnia populacji jest oznaczona jako μ. Średnia próbki jest zmienną losową, podczas gdy średnia populacji jest nieznaną stałą.

