Różnica między liczbami rzeczywistymi a liczbami całkowitych

Matematycy opracowali systemy, aby określić, w jaki sposób określona liczba różni się od innej. Podobnie jak inne koncepcje, kategorie liczb się nakładają. Ponieważ liczby rzeczywiste obejmują wszystkie liczby racjonalne, takie jak liczby całkowite, mają podobne cechy, takie jak wykorzystanie liczb całkowitych i wykreślanie na linii liczbowej. Stąd kluczowa różnica polega na tym, że liczby rzeczywiste są klasyfikacją ogólną, podczas gdy liczby całkowite są podzbiorem, który jest charakteryzowany jako liczby całkowite, które mogą mieć właściwości ujemne.

Jakie są liczby rzeczywiste?

Liczby rzeczywiste to wartości, które można znaleźć na linii liczbowej, która jest zwykle wyrażona jako geometryczna pozioma linia, w której wybrany punkt działa jako „pochodzenie”. Te, które spadają po prawej stronie, są oznaczone jako pozytywne, podczas gdy te po lewej są ujemne. Opis „Real” został przedstawiony przez Rene Descartes, słynny matematyk i filozof w XVII wieku. Szczególnie ustanawia różnicę między prawdziwymi korzeniami wielomianów a ich wyimaginowanymi korzeniami.

Liczby rzeczywiste obejmują liczby całości, liczby całkowite, naturalne, racjonalne i irracjonalne:

• Wszystkie liczby

Liczby całkowite to liczby dodatnie, które nie mają części ułamkowych ani punktów dziesiętnych, ponieważ reprezentują całe obiekty bez fragmentów lub kawałków.

• Liczby całkowite

Liczby całkowite to liczby, które obejmują ujemną stronę linii liczbowej.

• Liczby naturalne

Znane również jako liczby zliczające, liczby naturalne są jak liczby całkowite, ale zero nie jest uwzględnione, ponieważ nic nie można liczyć jako „0”.

• Liczby wymierne

Jeśli chodzi o swoje pochodzenie, Pitagoras, starożytny grecki matematyk ogłosił, że wszystkie liczby były racjonalne. Racjonalne liczby to iloraz lub ułamki dwóch liczb całkowitych.  Gdzie P i Q są zarówno liczbowymi, jak i Q nie są równoważne zero, P/Q jest liczbą racjonalną. Na przykład 3/5 to liczba racjonalna, ale 3/0 nie jest.

• Irracjonalne liczby

Student Pitagorasa, Hippasus, nie zgodził się, że wszystkie liczby były racjonalne. Poprzez geometrię udowodnił, że niektóre liczby były irracjonalne. Na przykład pierwiastek kwadratowy dwóch, który wynosi 1.41 nie można wyrazić jako ułamka; Stąd jest irracjonalne. Niestety, rzeczywistość racjonalnych liczb nie została zaakceptowana przez wyznawców Pitagorasa. Spowodowało to, że Hippaza utonęła na morzu, co w tym czasie mówi się, że jest karą od Bogów.

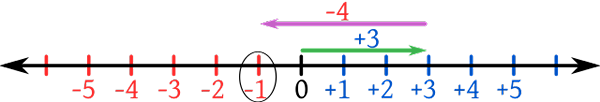
Co to są liczby całkowite?

Od łacińskiego słowa „liczba całkowita”, które tłumaczy się na „całość” lub „nietknięte”, liczby te nie mają komponentów ułamkowych ani dziesiętnych, podobnie jak liczby całe. Liczby obejmują dodatnie liczby naturalne lub liczby liczące i ich negatywy. Na przykład -3, -2, -1, 0, -1, 2, 3 są liczbami całkowitych. Zwykłą ilustracją są równie rozmieszczone liczby na nieskończonej linii liczbowej z zero, która nie jest ani pozytywna, ani ujemna, pośrodku. Stąd pozytywne są większe niż negatywy.

Jeśli chodzi o jego historię, następujące konta śledzą, w jaki sposób liczby całkowite zostały po raz pierwszy wykorzystane:

• W 200 b.C. Liczby ujemne zostały po raz pierwszy reprezentowane za pomocą czerwonych prętów w starożytnych Chinach.
• W około 630 A.D., Liczby ujemne zastosowano do reprezentowania długu w Indiach.
• Arbermouth Holst, niemiecki matematyk wprowadził liczby całkowite w 1563 r. Jako system i mnożenie. Opracował system jako odpowiedź na rosnącą liczbę królików i słoni, na których eksperymentował.

Poniżej przedstawiono cechy liczb całkowitych:

• Pozytywny

Liczby po prawej stronie linii liczbowej są dodatnie i często reprezentują wyższą wartość swoich ujemnych odpowiedników.

• Negatywny

Liczby po lewej stronie linii liczbowej są często postrzegane jako mniejsza standardowa wartość ich dodatnich odpowiedników.

• Neutralny

Środek linii liczbowej, zero jest liczbą całkowitą, która nie jest ani pozytywna ani ujemna.

• Brak fragmentów

Podobnie jak liczby całkowite, liczby całkowite nie mają punktów dziesiętnych ani ułamków.

Różnica między liczbami rzeczywistymi a liczbami całkowitych

Zakres liczb rzeczywistych i liczb całkowitych

Liczby rzeczywiste obejmują liczby liczb całkowitych, racjonalnych, irracjonalnych, naturalnych i refleksji. Z drugiej strony zakres liczb całkowitych dotyczy głównie liczb całkowitych, które są ujemne i pozytywne. Stąd liczby rzeczywiste są bardziej ogólne.

Frakcje

Liczby rzeczywiste mogą obejmować ułamki, takie jak liczby racjonalne i irracjonalne. Jednak ułamki nie mogą być liczbowymi.

Własność oparta na najmniejszym stopie

Liczby rzeczywiste mają najmniejszą pozycję, która jest również znana jako „kompletność”. Oznacza to, że liniowy zestaw liczb rzeczywistych ma podzbiory o cechach supremum.  Przeciwnie, liczby całkowite nie mają właściwości związanej z najmniej.

Własność archimedeńska

Właściwość Archimedean, która jest założeniem, że istnieje liczba naturalna, która jest równa lub większa niż jakakolwiek liczba rzeczywista, może być zastosowana do liczb rzeczywistych. Przeciwnie, właściwość Archimedean nie może być stosowana do liczb całkowitych.

Pole

Liczby rzeczywiste są rodzajem pola, które jest niezbędną strukturą algebraiczną, w której definiowane są procesy arytmetyczne. Przeciwnie, liczby całkowite nie są uważane za pole.

Policzalny

Jako zestaw liczba rzeczywistych jest niezliczona, podczas gdy liczby całkowite są policzalne.

Symbole liczb rzeczywistych i liczb całkowitych

Liczby rzeczywiste są symbolizowane jako „R”, podczas gdy zestaw liczb całkowitych jest symbolizowany jako „Z”.  N. Bourbaki, grupa francuskich matematyków w latach 30. XX wieku, określała „Z” od niemieckiego słowa „Zahlen”, co oznacza liczbę lub liczby całkowite.

Pochodzenie słów dla rzeczywistych liczb i liczb całkowitych

Liczby rzeczywiste oznaczały prawdziwe korzenie wielomianów, podczas gdy liczba całkowita pochodzi od łacińskiego słowa, „całości”, ponieważ nie zawierają dziesiętnych ani ułamków.

Liczby rzeczywiste vs liczby całkowite

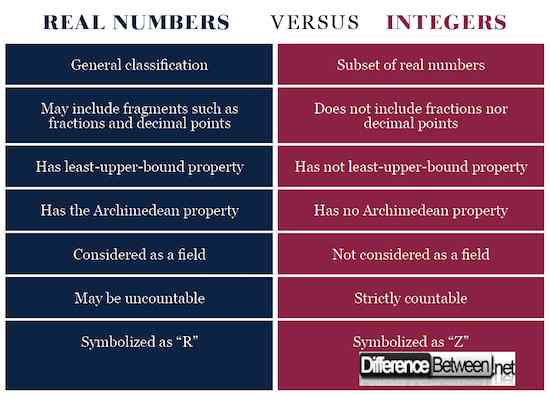
Podsumowanie liczb rzeczywistych vs.  Liczby całkowite

• Zarówno liczby rzeczywiste, jak i liczby całkowite można wykreślić na linii liczbowej.
• Liczby całkowite to podzbiór liczb rzeczywistych.
• Liczby całkowite mają liczby ujemne.
• Jako zestaw liczby rzeczywiste mają bardziej ogólny zakres w porównaniu do liczb całkowitych.
• W przeciwieństwie do liczb całkowitych, liczby rzeczywiste mogą obejmować ułamki i punkty dziesiętne.
• Właściwości najmniej opartej, archimedejskiej i dziedzinie są ogólnie stosowane do liczb rzeczywistych, ale nie do liczb całkowitych.
• W przeciwieństwie do liczb rzeczywistych, liczby całkowite są ściśle policzalne.
• „R” oznacza rzeczywiste liczby, podczas gdy „Z” jest dla liczb całkowitych.