Różnica między wzajemnie wykluczającymi się wydarzeniami
- 695
- 38
- Łukasz Kalisz
 Prawdopodobieństwo jest koncepcją matematyczną, która stała się teraz pełnoprawną dyscypliną i jest istotną częścią statystyki. Losowy eksperyment w prawdopodobieństwie to wydajność, która generuje określony wynik, wyłącznie oparty na szansy. Wyniki losowego eksperymentu nazywane są zdarzeniem. Prawdopodobnie istnieją różne rodzaje zdarzeń, jak w prostym, złożonym, wzajemnie wykluczającym się, wyczerpującym, niezależnym, zależnym, równie prawdopodobnym itp. Kiedy zdarzenia nie mogą wystąpić w tym samym czasie, są one wezwane wzajemnie się wykluczające
Prawdopodobieństwo jest koncepcją matematyczną, która stała się teraz pełnoprawną dyscypliną i jest istotną częścią statystyki. Losowy eksperyment w prawdopodobieństwie to wydajność, która generuje określony wynik, wyłącznie oparty na szansy. Wyniki losowego eksperymentu nazywane są zdarzeniem. Prawdopodobnie istnieją różne rodzaje zdarzeń, jak w prostym, złożonym, wzajemnie wykluczającym się, wyczerpującym, niezależnym, zależnym, równie prawdopodobnym itp. Kiedy zdarzenia nie mogą wystąpić w tym samym czasie, są one wezwane wzajemnie się wykluczające
Z drugiej strony, jeśli każde zdarzenie nie mają wpływu na inne zdarzenia, są one wezwane niezależne wydarzenia. Przeczytaj pełny artykuł przedstawiony poniżej, aby lepiej zrozumieć różnicę między wzajemnie wykluczającymi się wydarzeniami i niezależnymi wydarzeniami.
Treść: Wykluczające się wzajemnie wydarzenie a niezależne wydarzenie
- Wykres porównania
- Definicja
- Kluczowe różnice
- Wniosek
Wykres porównania
| Podstawa do porównania | Zdarzeń wzajemnie wykluczających | Niezależne wydarzenia |
|---|---|---|
| Oznaczający | Mówi się, że dwa wydarzenia wykluczają się wzajemnie, gdy ich występowanie nie jest jednocześnie. | Mówi się, że dwa zdarzenia są niezależne, gdy występowanie jednego zdarzenia nie może kontrolować występowania innych. |
| Wpływ | Występowanie jednego zdarzenia spowoduje brak występowania drugiego. | Występowanie jednego zdarzenia nie będzie miało wpływu na wystąpienie drugiego. |
| Matematyczna formuła | P (a i b) = 0 | P (a i b) = p (a) p (b) |
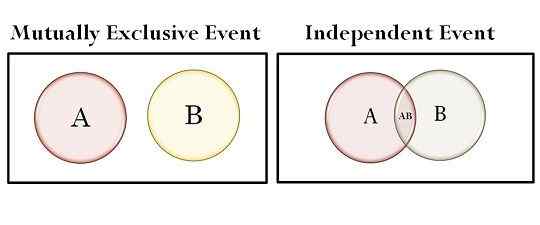
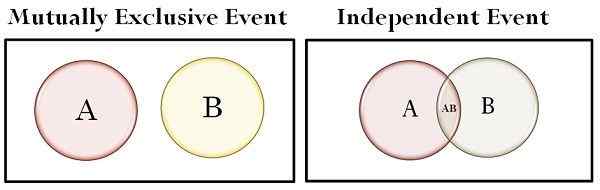
| Zestawy na schemacie Venna | Nie nakłada się | Nakładania się |
Definicja wydarzenia wykluczającego się wzajemnie
Zdarzenia wykluczające się wzajemnie to te, które nie mogą występować jednocześnie, ja.mi. gdzie wystąpienie jednego zdarzenia powoduje brak występowania drugiego zdarzenia. Takie wydarzenia nie mogą być prawdziwe w tym samym czasie. Dlatego wydarzenie jednego wydarzenia uniemożliwia inne wydarzenie. Są one również znane jako zdarzenia rozłączne.
Weźmy przykład rzucania monety, w której wynik byłby albo głowa lub ogon. Zarówno głowa, jak i ogon nie mogą występować jednocześnie. Weź kolejny przykład, załóżmy, że jeśli firma chce kupić maszyny, dla których ma dwie opcje maszyny A i B. Maszyna, która jest opłacalna, a wydajność jest lepsza, zostanie wybrana. Akceptacja maszyny A automatycznie spowoduje odrzucenie maszyny B i odwrotnie.
Definicja niezależnego zdarzenia
Jak sama nazwa wskazuje, niezależne zdarzenia są zdarzeniami, w których prawdopodobieństwo jednego zdarzenia nie kontroluje prawdopodobieństwa wystąpienia drugiego zdarzenia. Happen lub niehapowanie takiego zdarzenia nie ma absolutnie żadnego wpływu na wydarzenie lub brak happelingu innego wydarzenia. Produkt ich oddzielnych prawdopodobieństw jest równy prawdopodobieństwu, że oba zdarzenia wystąpią.
Weźmy przykład, załóżmy, że jeśli moneta zostanie rzucona dwukrotnie, ogon w pierwszej szansy i ogonie w drugiej, wydarzenia są niezależne. Kolejny przykład tego, załóżmy, że jeśli kostka zostanie podłączona dwukrotnie, 5 w pierwszej szansy i 2 w drugiej, zdarzenia są niezależne.
Kluczowa różnica między wzajemnie wykluczającymi się wydarzeniami
Istotne różnice między zdarzeniami wzajemnie wykluczającymi się i niezależnymi są opracowane jako pod:
- Wydarzenia wzajemnie wykluczające się są wydarzeniami, gdy ich występowanie nie jest jednocześnie. Gdy wystąpienie jednego zdarzenia nie może kontrolować występowania innych, takie zdarzenia nazywane są zdarzeniem niezależnym.
- W zdarzeniach wzajemnie wykluczających się, występowanie jednego zdarzenia spowoduje brak występowania drugiego. I odwrotnie, w niezależnych zdarzeniach występowanie jednego zdarzenia nie będzie miało wpływu na wystąpienie drugiego.
- Zdarzenia wykluczające się wzajemnie są reprezentowane matematycznie jako p (a i b) = 0, podczas gdy zdarzenia niezależne są reprezentowane jako p (a i b) = p (a) p (b).
- Na schemacie Venna zestawy nie pokrywają się ze sobą, w przypadku wzajemnie wykluczających się wydarzeń, podczas gdy mówimy o niezależnych wydarzeniach, zestawy nakładają się.
Wniosek
Tak więc, dzięki powyższej dyskusji, jasne jest, że oba wydarzenia nie są takie same. Co więcej, należy pamiętać, a to znaczy, jeśli zdarzenie wyklucza się wzajemnie, to nie może być niezależne i odwrotnie. Jeśli dwa zdarzenia A i B wykluczają się wzajemnie, można je wyrazić jako p (aub) = p (a)+p (b), podczas gdy jeśli te same zmienne są niezależne, wówczas można je wyrazić jako p (a∩b) = P (a) p (b).

