Różnica między średnią a medianą

- 4663
- 1208
- Hilarion Porębski
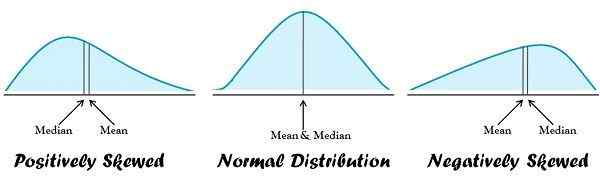 Tendencja centralna implikuje tendencję punktów danych do klastra wokół jej centralnej lub średnich wartości. Dwie najczęściej stosowane miary tendencji centralnej są średnie i mediana. Mieć na myśli jest definiowany jako „centralna” wartość danego zestawu danych, podczas gdy mediana jest wartością „średnim” w danym zestawie danych.
Tendencja centralna implikuje tendencję punktów danych do klastra wokół jej centralnej lub średnich wartości. Dwie najczęściej stosowane miary tendencji centralnej są średnie i mediana. Mieć na myśli jest definiowany jako „centralna” wartość danego zestawu danych, podczas gdy mediana jest wartością „średnim” w danym zestawie danych.
Idealną miarą tendencji centralnej jest wyraźnie zdefiniowana, łatwo zrozumiana, po prostu obliczalna. Powinien opierać się na wszystkich obserwacjach, a najmniej dotkniętych ekstremalnymi obserwacjami obecnymi w zestawie danych.
Ludzie często kontrastują z tych dwóch środków, ale faktem jest, że są różne. Ten artykuł konkretnie podkreśla podstawowe różnice między średnią a medianą. Spójrz.
Treść: średnia vs mediana
- Wykres porównania
- Definicja
- Kluczowe różnice
- Przykład
- Wniosek
Wykres porównania
| Podstawa do porównania | Mieć na myśli | Mediana |
|---|---|---|
| Oznaczający | Średnia odnosi się do prostej średniej danego zestawu wartości lub ilości. | Mediana jest zdefiniowana jako liczba środkowa na uporządkowanej liście wartości. |
| Co to jest? | To średnia arytmetyczna. | Jest to średnia pozycyjna. |
| Reprezentuje | Środek ciężkości zestawu danych | Środek ciężkości zestawu danych Środkowy punkt zestawu danych |
| Zastosowanie | Normalna dystrybucja | Dystrybucja wypaczenia |
| Wartości odstające | Średnia jest wrażliwa na wartości odstające. | Mediana nie jest wrażliwa na wartości odstające. |
| Obliczenie | Średnia jest obliczana przez dodanie wszystkich obserwacji, a następnie podzielenie wartości uzyskanej z liczbą obserwacji. | Aby obliczyć medianę, zestaw danych jest ułożony w kolejności rosnącej lub malejącej, a następnie wartość należącą do dokładnego środka nowego zestawu danych, jest mediana. |
Definicja średniej
Średnia jest szeroko stosowaną miarą tendencji centralnej, która zdefiniowana jako średnia zbioru wartości. Reprezentuje model i najczęstszą wartość danego zakresu wartości. Można go obliczyć, zarówno w seriach dyskretnych, jak i ciągłych.
Średnia jest równa sumie wszystkich obserwacji podzielonych przez liczbę obserwacji w zestawie danych. Jeśli wartość przyjęta przez zmienną jest równa, jej średnia będzie również sama. Średnia może być dwóch rodzajów, średnia próbki (x̅) i średnia populacji (µ). Można go obliczyć za pomocą podanego wzoru:
- Średnia arytmetyczna:
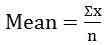 gdzie ʃ = grecka litera sigma, oznacza „sumę…”
gdzie ʃ = grecka litera sigma, oznacza „sumę…”
n = liczba wartości - Dla serii dyskretnych:
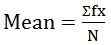 gdzie, f = częstotliwość
gdzie, f = częstotliwość - Dla ciągłych porcji:
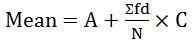 gdzie d = (x-a)/c
gdzie d = (x-a)/c
A = Zakładana średnia
C = wspólny dzielnik
Definicja mediany
Mediana jest kolejną ważną miarą tendencji centralnej, używanej do podziału wartości na dwie równe części, i.mi. Większa połowa próby, populacji lub rozkładu prawdopodobieństwa od dolnej połowy. Jest to wartość w środku, która jest osiągana, gdy obserwacje są sortowane w określonej kolejności, albo kolejność rosnąca lub malejąca.
W celu obliczenia mediany, przede wszystkim ułóż obserwacje w najniższym do najwyższego lub najwyższego do najniższego, a następnie zastosuj odpowiedni wzór, zgodnie z warunkami podano poniżej:
- Jeśli liczba obserwacji jest dziwna:
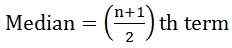 gdzie n = liczba obserwacji
gdzie n = liczba obserwacji - Jeśli liczba obserwacji Jest nawet:
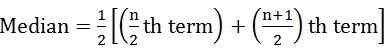
- Dla serii ciągłych:
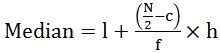 gdzie l = dolna granica klasy mediany
gdzie l = dolna granica klasy mediany
C = skumulowana częstotliwość poprzedniej klasy mediany
f = częstotliwość klasy mediany
H = szerokość klasy
Kluczowe różnice między średnią i medianą
Istotne różnice między średnią a medianą przedstawiono w artykule podanym poniżej:
- W statystykach średnia jest zdefiniowana jako prosta średnia z danego zestawu wartości lub ilości. Mówi się, że mediana jest liczbą środkową na uporządkowanej liście wartości.
- Chociaż średnia jest średnią arytmetyczną, mediana jest w zasadzie średniej pozycji, pozycja zestawu danych określa wartość mediany.
- Średnia przedstawia środek ciężkości zestawu danych, podczas gdy mediana podkreśla średnią wartość zestawu danych.
- Średnia jest odpowiednia dla danych normalnie rozproszonych. Z drugiej strony mediana jest najlepsza, gdy rozkład danych jest wypaczony.
- Na średnią jest wysoce wpływ ekstremalna wartość, której nie ma w przypadku mediany.
- Średnia jest obliczana przez dodanie wszystkich obserwacji, a następnie podzielenie wartości uzyskanej z liczbą obserwacji; Wynik jest średni. W przeciwieństwie do mediany, zestaw danych jest ułożony w kolejności rosnącej lub malejącej, a następnie wartość, która wpadnie w dokładny środek nowego zestawu danych, jest mediana.
Przykład
Znajdź średnią i medianę podanego zestawu danych:
58, 26, 65, 34, 78, 44, 96
Rozwiązanie: Aby obliczyć średnio, musisz podzielić sumę obserwacji z liczbą obserwacji,
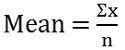
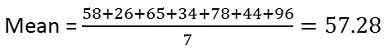 Średnia = 57.28
Średnia = 57.28
Aby obliczyć medianę, przede wszystkim ułóż serię w sekwencji, i.mi. najniższy do najwyższego,
26, 34, 44, 58, 65, 78, 96
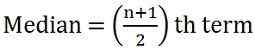 gdzie n = liczba obserwacji
gdzie n = liczba obserwacji
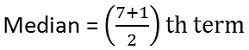 Mediana = 4th Termin = 58
Mediana = 4th Termin = 58
Wniosek
Po przejrzeniu powyższych punktów możemy powiedzieć, że te dwa koncepcje matematyczne są różne. Średnia lub średnia arytmetyczna jest uważana za najlepszą miarę tendencji centralnej, ponieważ zawiera wszystkie cechy idealnej miary, ale ma jedną wadę, że fluktuacje próbkowania wpływają na średnią.
W ten sam sposób mediana jest również jednoznacznie zdefiniowana i łatwa do zrozumienia i obliczenia, a najlepszą rzeczą w tym środku jest to, że nie mają wpływu fluktuacje próbkowania, ale jedyną wadą mediany jest to, że nie opiera się ona na wszystkich obserwacje. W przypadku klasyfikacji otwartych mediana jest zwykle preferowana od średniej.

