Różnica między CODOMAIN a zakresem

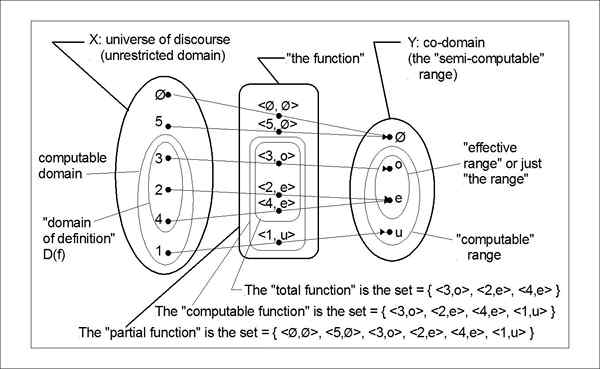
Zarówno CODOMAIN, jak i zakres to pojęcia funkcji stosowanych w matematyce. Chociaż oba są związane z wyjściem, różnica między nimi jest dość subtelna. Termin „zakres” jest czasami używany w odniesieniu do „Codomain”.  Po rozróżnieniu między nimi możesz odwołać się do CODOMAIN jako wyjścia, że ​​funkcja jest zadeklarowana do wytworzenia. Zakres terminu jest jednak niejednoznaczny, ponieważ może być czasem używany dokładnie tak, jak używany jest CODOMAIN. Weźmy F: A -> b, gdzie F jest funkcją od A do B. Następnie B jest kodomą funkcji „F”, A zakres to zestaw wartości, które funkcja przyjmuje, co jest oznaczone przez F (A). Zakres może być równy lub mniej niż codomain, ale nie może być większy niż to.

Na przykład niech a = 1, 2, 3, 4, 5 i b = 1, 4, 8, 16, 25, 64, 125. Funkcja F: A -> b jest zdefiniowane przez F (x) = x ^3. Więc tu,

Domain = ustaw a

Codomain = set b, i

Zakres (r) = 1, 8, 64, 125

Zakres powinien być sześcianem zestawu A, ale kostka 3 (to 27) nie jest obecna w zestawie B, więc mamy 3 w domenie, ale nie mamy 27 ani w CODOMAIN, ani w zakresie. Zakres jest podzbiorem Codomain.

Co to jest codomain funkcji?

„Codomain” funkcji lub relacji jest zestawem wartości, które mogą z niej wyjść. W rzeczywistości jest to część definicji funkcji, ale ogranicza dane wyjściowe funkcji. Na przykład weźmy notację funkcji F: R -> r. To znaczy, że F jest funkcją od liczb rzeczywistych do liczb rzeczywistych. Tutaj Codomain jest zbiorem liczb rzeczywistych r lub zestawem możliwych wyjść, które z niego wychodzą. Domena to także zestaw liczb rzeczywistych r. Tutaj możesz również określić funkcję lub relację, aby ograniczyć wszelkie wartości ujemne, które wytwarzają wyjście. Mówiąc prosto, CODOMAIN jest zbiorem, w którym spadają wartości funkcji.

Niech n będzie zbiorem liczb naturalnych, a relacja jest zdefiniowana jako r = (x, y): y = 2x, x, y ∈ N

Tutaj, x i y są zawsze liczbami naturalnymi. Więc,

Domena = n i

CODOMAIN = n, czyli zbiór liczb naturalnych.

Jaki jest zakres funkcji?

„Zakres” funkcji jest określany jako zestaw wartości, które wytwarza lub po prostu jako zestaw wyjściowy jej wartości. Zakres terminu jest często używany jako Codomain, jednak w szerszym znaczeniu termin jest zarezerwowany dla podzbioru Codomain. Mówiąc prosto, zakres jest zestawem wszystkich wartości wyjściowych funkcji, a funkcja jest korespondencją między domeną a zakresem. W teorii zestawu natywnego zasięg odnosi się do obrazu funkcji lub kodomenu funkcji. W współczesnej matematyce zasięg jest często używany w odniesieniu do obrazu funkcji. Starsze książki odnoszą się do tego, co obecnie zwane CODOMAIN i Modern Books zwykle używają terminu, aby odnosić się do tego, co jest obecnie znane jako obraz. Większość książek w ogóle nie używa zasięgu słów, aby całkowicie uniknąć zamieszania.

Na przykład niech a = 1, 2, 3, 4 i b = 1, 4, 9, 25, 64. Funkcja F: A -> b jest zdefiniowane przez F (x) = x ^2. Więc tutaj, ustaw A jest domeną, a zestaw B to Codomain, a zakres = 1, 4, 9. Zakres jest kwadratem A jak zdefiniowany przez funkcję, ale kwadrat 4, który wynosi 16, nie jest obecny ani w CODOMAN, ani w zakresie.

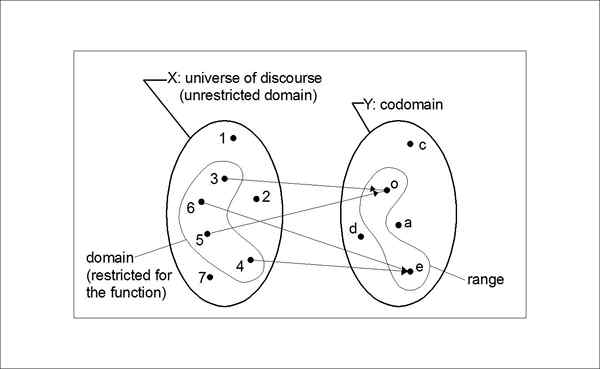
Różnica między CODOMAIN a zakresem

Definicja Codomain i zakresu

Oba terminy są powiązane z wyjściem funkcji, ale różnica jest subtelna. Podczas gdy Codomain funkcji jest zestawem wartości, które mogą z niej wyjść, jest to w rzeczywistości część definicji funkcji, ale ogranicza dane wyjściowe funkcji. Z drugiej strony zakres funkcji odnosi się do zestawu wartości, które faktycznie wytwarza.

Cel Codomain and Range

Codomain funkcji to zestaw wartości obejmujący zakres, ale może zawierać niektóre dodatkowe wartości. Celem CODOMAIN jest ograniczenie wyjścia funkcji. Czasami może być trudny do określania, ale większy zestaw wartości obejmujący cały zakres można określić. Codomain funkcji czasami ma ten sam cel co zakres.

Przykład Codomain i zakresu

Jeśli a = 1, 2, 3, 4 i b = 1, 2, 3, 4, 5, 6, 7, 8, 9 i relacja F: A -> b jest zdefiniowane przez F (x) = x ^2, a następnie CODOMAIN = SET B = 1, 2, 3, 4, 5, 6, 7, 8, 9 i zakres = 1, 4, 9. Zakres jest kwadratem zestawu A, ale kwadrat 4 (czyli 16) nie jest obecny w żadnym zestawie B (codomain) lub w zakresie.

CODOMAIN vs. Zakres: wykres porównawczy

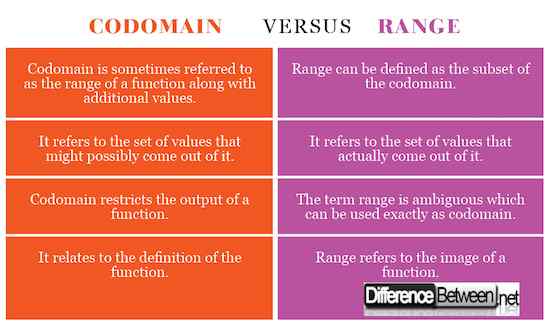
Podsumowanie CODOMAIN VS. Zakres

Chociaż oba są powszechnymi terminami stosowanymi w natywnej teorii zestawu, różnica między nimi jest dość subtelna. Codomain funkcji można po prostu nazwać zestawem jej możliwych wartości wyjściowych. W kategoriach matematycznych jest to zdefiniowane jako wyjście funkcji. Z drugiej strony zakres funkcji można zdefiniować jako zestaw wartości, które faktycznie z niej wychodzą. Jednak termin jest niejednoznaczny, co oznacza, że ​​można go czasem używać dokładnie jako CODOMAIN. Jednak w współczesnej matematyce zasięg jest opisywany jako podzbiór Codomain, ale w znacznie szerszym sensie.