Różnica między związkiem a skrzyżowaniem

Przed zrozumieniem różnicy między dwoma ustalonymi operatorami związkiem i przecięciem, zrozummy najpierw pojęcie teorii ustalonej. Zestaw teoria jest podstawową gałęzią matematyki, która bada zestawy, szczególnie niezależnie od tego, czy obiekt należy lub nie należy do zestawu obiektów, które są w jakiś sposób istotne matematyki. Zestaw jest zasadniczo zbiorem dobrze zdefiniowanych obiektów, które mogą mieć znaczenie matematyczne, takie jak liczby lub funkcje. Obiekty w zestawie nazywane są elementami, które mogą być jak liczby, ludzie, samochody, stany itp. Prawie wszystko i dowolną liczbę elementów można zebrać razem, aby utworzyć zestaw.

Mówiąc prosto, SET to zbiór dowolnej liczby nieo -uporządkowanych elementów, które można uznać za pojedynczy obiekt jako całość. Zrozum podstawowe pojęcia i zapis z zestawu oraz sposób jego reprezentowania. Wszystko zaczyna się od binarnej relacji między obiektem x a zestawem a. Reprezentować, jeśli x jest członkiem zestawu a, używa się notacji x ∊ a, podczas gdy x ∉ a wskazuje, że obiekt x nie należy do zestawu a. Członek zestawu jest wymieniony w ramach klastrowych. Na przykład zestaw liczb pierwszych mniej niż 10 można zapisać jako 2, 3, 5, 7. Podobnie, zestaw liczb parzystych mniej niż 10 można zapisać jako 2, 4, 6, 8. Hipotetycznie, prawie każdy skończony zestaw może być reprezentowany przez jego członków.

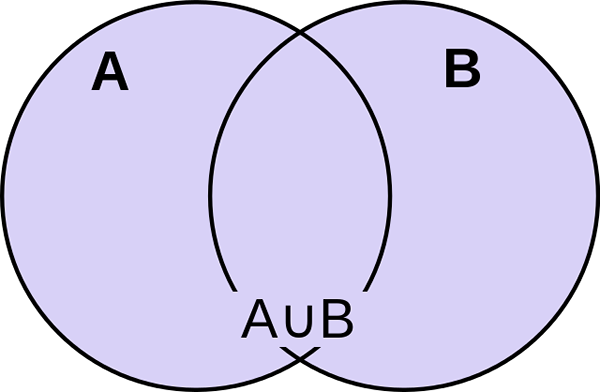
Co to jest związek setek?

Związek dwóch zestawów a i b jest zdefiniowany jako zestaw elementów należących do A lub B, lub ewentualnie obu. Jest po prostu zdefiniowany jako zestaw wszystkich odrębnych elementów lub członków, w których członkowie należą do dowolnego z tych zestawów. Operator Unii odpowiada logicznemu lub reprezentowanemu przez symbol ∪. Jest to najmniejszy zestaw zawierający wszystkie elementy obu zestawów. Na przykład, jeśli zestaw A wynosi 1, 2, 3, 4, 5 i zestaw B wynosi 3, 4, 6, 7, 9, wówczas związek A i B jest reprezentowany przez A∪b i jest pisany jako 1, 2, 3, 4, 5, 6, 7, 9. Ponieważ liczby 3 i 4 są obecne w obu zestawach A i B, nie ma potrzeby ich podawać dwa razy. Oczywiste jest, że liczba elementów związku A i B jest mniejsza niż suma poszczególnych zestawów, ponieważ niewiele liczb jest powszechnych w obu zestawach.

A = 1, 3, 5, 7, 9

B = 3, 6, 9, 12, 15

A∪b = 1, 3, 5, 6, 7, 9, 12, 15

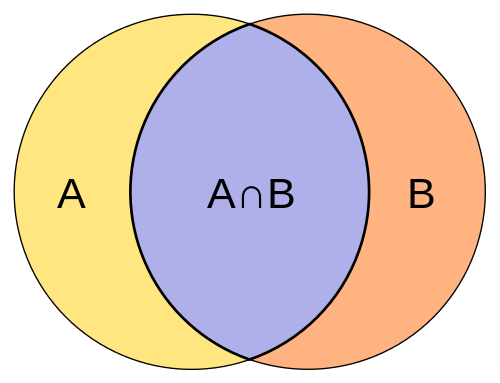
Co to jest przecięcie zestawów?

Przecięcie dwóch zestawów a i b jest zdefiniowane jako zestaw elementów należących zarówno do A i B. Jest po prostu zdefiniowany jako zestaw zawierający wszystkie elementy zestawu A, który również należą do zestawu B, i podobnie wszystkie elementy zestawu B należą do zestawu A. Operator przecięcia odpowiada logicznemu i jest reprezentowany przez symbol ∩. Przeciwnie, przecięcie dwóch zestawów jest największym zestawem zawierającym wszystkie elementy wspólne dla obu zestawów. Na przykład, jeśli zestaw A wynosi 1, 2, 3, 4, 5 i zestaw B wynosi 3, 4, 6, 7, 9, to przecięcie a i b jest reprezentowane przez A∩b i jest pisane i jest pisane jako 3, 4. Ponieważ tylko liczby 3 i 4 są powszechne w obu zestawach a i b, nazywane są przecięciem zestawów.

A = 2, 3, 5, 7, 11

B = 1, 3, 5, 7, 9, 11

A∩b = 3, 5, 7, 11

Różnica między związkiem a przecięciem zestawów

1. Podstawowy - Związek dwóch zestawów A i B jest zdefiniowany jako zestaw elementów należących do A lub B, lub być może oba, podczas gdy przecięcie dwóch zestawów jest zdefiniowane jako zestaw elementów należących do A i B.
2. Reprezentacja symboliczna - Związek dwóch zestawów jest reprezentowany przez symbol „∪”, podczas gdy przecięcie dwóch zestawów jest reprezentowane przez symbol „∩”.
3. Logiczne znaczenie - Związek dwóch zestawów odpowiada logicznej „lub”, podczas gdy przecięcie dwóch zestawów odpowiada logicznemu „i”.
4. Przykład - Niech a = a, e, i, o, u i

B = A, B, C, D, E, F

A∪b = a, b, c, d, e, f, i, o, u

A∩b = a, e

Union vs. Przecięcie: wykres porównawczy

Podsumowanie Unii vs. Skrzyżowanie

Zarówno związek, jak i przecięcie to dwie podstawowe operacje, za pomocą których zestawy można łączyć i powiązać ze sobą. Jeśli chodzi o teorię ustaloną, związek jest zestawem wszystkich elementów, które są w zestawie lub w obu, podczas gdy przecięcie jest zbiorem wszystkich odrębnych elementów należących do obu zestawów. Związek dwóch zestawów A i B jest symbolizowany jako „A∪B”, podczas gdy przecięcie A i B jest symbolizowane jako „A∩B”. Zestaw jest niczym innym jak zbiorem dobrze zdefiniowanych obiektów, takich jak liczby i funkcje, a obiekty w zestawie są wywoływane jako elementy.