Różnica między wariancją próbki a wariancją populacji

Wyjaśnienie

W statystykach termin pobieranie próbek odnosi się do wyboru części zagregowanych danych statystycznych w celu uzyskania odpowiednich informacji o całości. Łączne lub całe informacje statystyczne na temat konkretnego charakteru wszystkich członków objętych dochodzeniem nazywa się „populacją” lub „wszechświatem”. (Das, n.G., 2010). Wybrana część populacji, która jest wykorzystywana do uzyskania cech populacji lub wszechświata, jest określana jako „próbka”. Populacja jest uznawana za poszczególne jednostki lub członków, a niektóre jednostki są zawarte w próbie. Całkowita liczba jednostek populacji nazywa się wielkością populacji, a próbka nazywa się wielkością próby. Populacja i próbka mogą być skończone lub nieskończone i podobnie mogą być istnienie lub hipotetyczne.

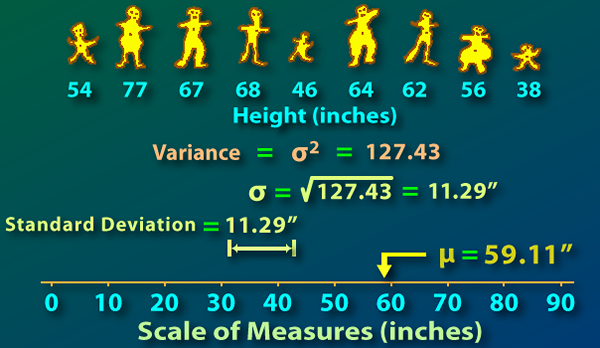
Zmienność: Wariancja jest wartością liczbową, która pokazuje, jak szeroko indywidualne dane w zestawie danych rozkładają się na temat średniej. Tak daleko jest każda liczba od średniej, a zatem od siebie. Wariancja wartości zerowej oznacza, że ​​wszystkie dane są identyczne. Bardziej wariancja, więcej są wartościami rozłożonymi na średniej, stąd od siebie nawzajem. Mniej wariancja, mniejsze wartości rozłożone na średnią, stąd od siebie, a wariancja nie może być ujemna.

Różnica między wariancją populacji a wariancją próbki

Główna różnica między wariancją populacji a wariancją próbki dotyczy obliczania wariancji. Wariancja jest obliczana w pięciu krokach. Pierwsza średnia jest obliczana, a następnie obliczamy odchylenia od średniej, a po trzecie odchylenia są kwadratowe, po czwarte, kwadratowe odchylenia są podsumowane i wreszcie suma ta jest podzielona przez liczbę elementów, dla których obliczana wariancja jest obliczana. Zatem wariancja = σ (xi-x-)/n. Gdzie xi = ith. Liczba, x- = średnia i n = liczba elementów…

Teraz, gdy wariancja ma być obliczona na podstawie danych populacji, n jest równe liczbie pozycji. Zatem jeśli należy obliczyć wariancję ciśnienia krwi wszystkich 1000 osób na podstawie danych na temat ciśnienia krwi wszystkich 1000 osób, wówczas n = 1000. Jednak gdy wariancja jest obliczana na podstawie danych przykładowych 1, przed podzieleniem sumę odchyleń kwadratowych. Zatem w powyższym przykładzie, jeśli przykładowe dane mają 100 pozycji, mianownik wynosiłby 100 - 1 = 99.

Z tego powodu wartość wariancji obliczonej na podstawie danych przykładowych jest wyższa niż wartość, którą można było znaleźć przy użyciu danych populacji. Logiką tego jest zrekompensowanie naszego braku informacji o danych populacji. Nie można znaleźć wariancji wysokości u ludzi, ponieważ nasz absolutny brak informacji o wysokości wszystkich żywych istot ludzkich, a nie mówienie o przyszłości. Nawet jeśli weźmiemy jeden umiarkowany przykład, taki jak dane o populacji na wysokości wszystkich żywych mężczyzn w nas, jest to fizycznie możliwe, ale koszt i czas w tym pokonałby cel jego obliczenia. Jest to powód, dla którego dane przykładowe są pobierane dla większości celów statystycznych, a towarzyszy temu brak informacji o większości danych. Aby to zrekompensować, wartość wariancji i odchylenia standardowego, który jest kwadratowym źródłem wariancji, jest wyższa w przypadku danych próbki niż wariancja danych populacji.

Działa to jako automatyczna tarcza dla analityków i decydentów. Logika dotyczy decyzji dotyczących budżetowania kapitałowego, finansowania osobistego i biznesowego, budownictwa, zarządzania ruchem i wielu odpowiednim dziedzinom. Pomaga to udziałowi w bezpiecznej stronie podczas podejmowania decyzji lub innych wniosków.

Streszczenie: Wariancja populacji odnosi się do wartości wariancji obliczonej na podstawie danych populacji, a wariancja próbki jest wariancją obliczoną na podstawie danych próbki. Ze względu na tę wartość mianownika w wzorze wariancji w przypadku danych przykładowych jest „n-1” i jest to „n” dla danych populacji. W rezultacie zarówno wariancja, jak i odchylenie standardowe pochodzące z danych próbnych są większe niż te, które odkryto na podstawie danych populacji.