Różnica między permutacją a kombinacją

- 901
- 4
- Pani — Jóźwiak
 W matematyce mogłeś usłyszeć pojęcia permutacji i łączenia liczby razy, ale czy kiedykolwiek wyobrażałeś sobie, że te dwa są różnymi pojęciami? Podstawową różnicą między permutacją a kombinacją jest kolejność obiektów, w permutacja Kolejność obiektów jest bardzo ważna, i.mi. Układ musi znajdować się w określonej kolejności liczby obiektów, biorących tylko niektóre lub wszystkie na raz.
W matematyce mogłeś usłyszeć pojęcia permutacji i łączenia liczby razy, ale czy kiedykolwiek wyobrażałeś sobie, że te dwa są różnymi pojęciami? Podstawową różnicą między permutacją a kombinacją jest kolejność obiektów, w permutacja Kolejność obiektów jest bardzo ważna, i.mi. Układ musi znajdować się w określonej kolejności liczby obiektów, biorących tylko niektóre lub wszystkie na raz.
Przeciwko temu, w przypadku połączenie, Zamówienie w ogóle nie ma znaczenia. Nie tylko w matematyce, ale także w życiu praktycznym, regularnie przechodzimy z tymi dwoma koncepcjami. Chociaż nigdy tego nie zauważamy. Więc przeczytaj uważnie artykuł, aby dowiedzieć się, jak te dwie koncepcje są różne.
Treść: Permutacja vs połączenie
- Wykres porównania
- Definicja
- Kluczowe różnice
- Przykład
- Wniosek
Wykres porównania
| Podstawa do porównania | Permutacja | Połączenie |
|---|---|---|
| Oznaczający | Permitacja odnosi się do różnych sposobów układania zestawu obiektów w kolejności sekwencyjnej. | Połączenie odnosi się do kilku sposobów wyboru przedmiotów z dużego zestawu obiektów, tak że ich porządek nie ma znaczenia. |
| Zamówienie | Odpowiedni | Nieistotny |
| Oznacza | Układ | Wybór |
| Co to jest? | Zamówione elementy | Zestawy nie zamówione |
| Odpowiedzi | Ile różnych układów można utworzyć z danego zestawu obiektów? | Ile różnych grup można wybrać z większej grupy obiektów? |
| Pochodzenie | Wiele permutacji z jednej kombinacji. | Pojedyncza kombinacja z pojedynczej permutacji. |
Definicja permutacji
Definiujemy permutację jako różne sposoby zorganizowania niektórych lub wszystkich członków zestawu w określonej kolejności. Implikuje wszystkie możliwe układ lub rearanżowanie danego zestawu, w wyróżniającą się kolejność.
Na przykład, Cała możliwa permutacja stworzona z liter x, y, z -
- Biorąc wszystkie trzy naraz to XYZ, XZY, YXZ, YZX, ZXY, ZYX.
- Biorąc dwa na raz, to XY, XZ, YX, YZ, ZX, ZY.
Całkowita liczba możliwych permutacji N rzeczy, pobranych R na raz, można obliczyć jako:
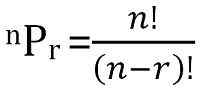
Definicja kombinacji
Połączenie jest definiowane jako różne sposoby, wyboru grupy, biorąc niektórych lub wszystkich członków zestawu, bez następującego zamówienia.
Na przykład, Wszystkie możliwe kombinacje wybrane z literą M, N, O -
- Gdy wybierane są trzy z trzech liter, jedyną kombinacją jest MNO
- Gdy mają być wybrane dwie z trzech liter, możliwe kombinacje to Mn, nie, om.
Całkowita liczba możliwych kombinacji N rzeczy, pobranych R na raz można obliczyć jako:
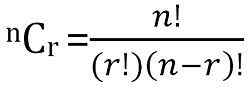
Kluczowe różnice między permutacją a kombinacją
Różnice między permutacją a kombinacją są wyraźnie rysowane z następujących podstaw:
- Termin permutacja odnosi się do kilku sposobów układania zestawu obiektów w kolejności sekwencyjnej. Połączenie implikuje kilka sposobów wyboru przedmiotów z dużej puli obiektów, tak że ich porządek jest nieistotny.
- Podstawowym punktem wyróżniającym te dwa koncepcje matematyczne jest porządek, umiejscowienie i pozycja, i.mi. W cechach permutacji wymienionych powyżej ma znaczenie, co nie ma znaczenia w przypadku kombinacji.
- Permutacja oznacza kilka sposobów na aranżowanie rzeczy, ludzi, cyfry, alfabetów, kolorów itp. Z drugiej strony kombinacja wskazuje na różne sposoby wyboru pozycji menu, jedzenia, ubrań, przedmiotów itp.
- Permutacja jest niczym innym jak uporządkowaną kombinacją, podczas gdy kombinacja implikuje zbiory nieopisane lub parowanie wartości w określonych kryteriach.
- Wiele permutacji można uzyskać z pojedynczej kombinacji. I odwrotnie, tylko jedną kombinację można uzyskać z pojedynczej permutacji.
- Permitacja odpowiada, ile różnych ustaleń można utworzyć z danego zestawu obiektów? W przeciwieństwie do kombinacji, która wyjaśnia, ile różnych grup można wybrać z większej grupy obiektów?
Przykład
Załóżmy, że istnieje sytuacja, w której musisz znaleźć całkowitą liczbę możliwych próbek dwóch z trzech obiektów a, b, c. W tym pytaniu przede wszystkim musisz zrozumieć, czy pytanie jest powiązane z permutacją lub kombinacją, a jedynym sposobem na znalezienie tego jest sprawdzenie, czy zamówienie jest ważne, czy nie.
Jeśli zamówienie jest znaczące, pytanie jest związane z permutacją, a możliwymi próbkami będą, AB, BA, BC, CB, AC, CA. Gdzie AB różni się od BA, BC różni się od CB, a AC jest inaczej.
Jeśli zamówienie jest nieistotne, pytanie jest powiązane z kombinacją, a możliwymi próbkami będą AB, BC i CA.
Wniosek
Dzięki powyższej dyskusji jasno wynika, że permutacja i kombinacja to różne terminy, które są wykorzystywane w matematyce, statystyce, badaniach i naszym codziennym życiu. Punktem, o którym należy pamiętać, w odniesieniu do tych dwóch koncepcji jest to, że dla danego zestawu obiektów permutacja będzie zawsze wyższa niż jej kombinacja.
- « Różnica między rachunkowością a audytem
- Różnica między wspólnym przedsięwzięciem a sojuszem strategicznym »

