Różnica między asymptotem poziomym i pionowym

Zanim przejdziemy do tematu asymptoteki poziomej i pionowej, spróbujmy zrozumieć, czym dokładnie są asymptoty i jaką rolę odgrywają w matematyce. W geometrii projekcyjnej asymptota jest linią prostą, która zbliża się do danej krzywej arbitralnie, ale nie spotyka się w żadnej skończonej odległości. Geometrycznie linia jest asymptotem krzywej y = f (x), jeśli odległość między linią a punktem „p” na krzywej zbliża się do zera, ponieważ x i y ma tendencję do nieskończoności. Wykres może mieć jedną asymptot równolegle do każdej osi. Właściwie asymptota jest czymś, czego nie ma fizycznie - to bardziej jak udawanie.

Asymptota pomaga określić działania lub kształty rzeczy, ale tak naprawdę nie jest to część wykresu. Jest to po prostu wyobraźnia, która pomaga wykresować funkcję racjonalną. Gdy krzywa zbliża się do asymptoty, zbliża się do asymptotu, ale nigdy nie dotyka. Zatem asymptota pomaga określić, gdzie wykres funkcji może lub nie może przejść. Biorąc to pod uwagę, istnieją trzy rodzaje asymptotów: asymptoty pionowe, poziome i ukośne. Ale omówimy tylko pionowe asymptoty i poziome asymptoty i zobaczymy, jak dowiedzieć się, co tak naprawdę.

Co to jest asymptotka pozioma?

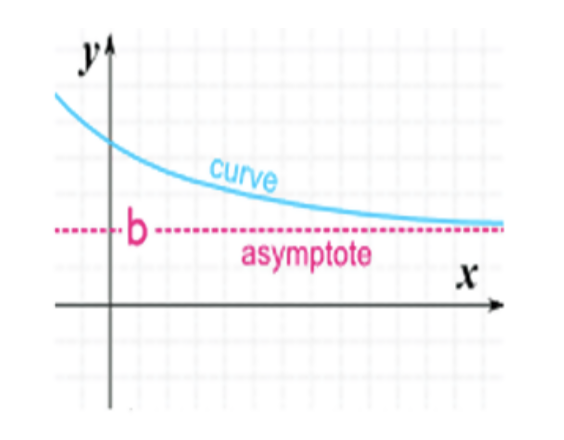
Asymptotka pozioma to stała wartość na wykresie, której funkcja zbliża się, ale tak naprawdę nie osiąga. Wskazuje, co faktycznie dzieje się z krzywą, ponieważ wartości X stają się bardzo duże lub bardzo małe. W powyższych przykładach graficznych krzywa zbliża się do stałej wartości B, ale tak naprawdę nigdy nie osiąga, y = 0.

Linia y = b jest poziomą asymptotem wykresu „f 'if f (x) -> b as x -> ∞ lub x -> -∞

Aby znaleźć poziomą asymptot funkcji racjonalnej, należy wziąć pod uwagę stopień wielomianu w licznikach i mianowniku.

• Jeśli mianownik ma najwyższą zmienną moc w równaniu funkcyjnym, poziome asymptotem jest automatycznie osi x lub y = 0.
• Jeśli zarówno licznik, jak i mianownik mają równy stopień, weź wiodące współczynniki tych terminów z najwyższą mocą i ułam je, aby znaleźć poziomą asymptotkę
• Jeśli licznik ma najwyższą zmienną moc w równaniu funkcji, funkcja nie ma poziomej asymptoteki; Wykres prawdopodobnie będzie miał ukośną asymptotkę.

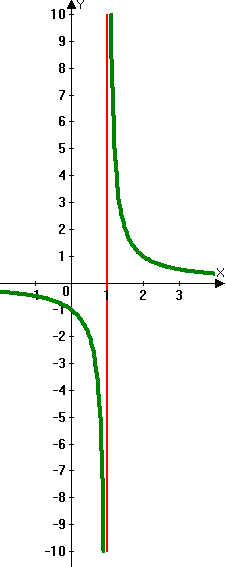
Co to jest asymptotka pionowa?

Ponieważ mianownik frakcji nigdy nie może być zerowy, posiadanie zmiennej na dole, jeśli ułamek może stanowić problem. Pewna wartość domeny „x” sprawia, że ​​mianownik zero i funkcja przeskakuje tę wartość na wykresie, tworząc pionową asymptotkę. Są to pionowe linie rysowane lekko lub z myślnikami, aby pokazać, że nie są częścią wykresu.

Jeśli liczba rzeczywista „A” to zero mianownika Q (x), to wykres f (x) = p (x)/q (x), gdzie p (x) i q (x) nie mają wspólnego czynniki, ma pionową asymptot, x = a.

Różnica między asymptotem poziomym i pionowym

Definicja

- Asymptotka pozioma to stała wartość na wykresie, której funkcja zbliża się, ale tak naprawdę nie osiąga. Wskazuje, co faktycznie dzieje się z krzywą, ponieważ wartości X stają się bardzo duże lub bardzo małe. Z drugiej strony pionowe asymptoty to niewidoczne linie pionowe, które odpowiadają zerowi w mianowniku frakcji racjonalnej. Są to pionowe linie rysowane lekko lub z myślnikami, aby pokazać, że nie są częścią wykresu.

Obliczenie

- Aby ustalić poziomą asymptot funkcji racjonalnej, należy wziąć pod uwagę stopień wielomianu w licznikach i mianownika. Jeśli mianownik ma najwyższą zmienną moc w równaniu funkcyjnym, poziome asymptotem jest automatycznie osi x lub y = 0. Jeśli zarówno licznik, jak i mianownik mają równy stopień, zrób ułamek swoich współczynników, aby określić poziome równanie asymptotu. Aby określić pionowe asymptoty funkcji racjonalnej, ustaw mianownik frakcji równy zero.

Przykład

- Dowiedzmy się o asymptotach funkcji

Y = 3x²+9x-21 ∕ x²-25

Aby znaleźć pionowe asymptoty, ustaw mianownik frakcji równy zero.

X²-25 = 0

(x-5) (x+5) = 0

x = 5 i x = - 5

Te dwie liczby to dwie wartości, których nie można uwzględnić w domenie, więc równania są asymptotami pionowymi. Tak więc dwa pionowe asymptoty to, x = 5 i x = - 5.

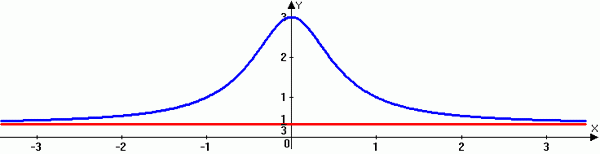
Teraz, aby ustalić poziomą asymptotkę, spójrz na oryginalne równanie. Tutaj najwyższa zmienna moc to 2. Ponieważ zarówno licznik, jak i mianownik mają taki sam stopień mocy, ułamek swoich współczynników:

y = 3x²/X²

y = 3/1

y = 3

Tak więc równanie poziomej asymptotu wynosi, y = 3.

Asymptota pozioma vs. Asymptota pionowa: wykres porównawczy

Podsumowanie poziomej asymptoteki vs. Pionowa asymptota

Asymptota pomaga określić działania lub kształty rzeczy, ale tak naprawdę nie jest to część wykresu. Pionowe asymptoty oznaczają miejsca, w których funkcja nie ma domeny. Rozwiązujesz równanie pionowych asymptotów, ustawiając mianownik frakcji równy zero. Z drugiej strony poziome asymptoty wskazują, co dzieje się z krzywą, ponieważ wartości x stają się bardzo duże lub bardzo małe. Aby znaleźć poziomą asymptot, musisz wziąć pod uwagę stopień wielomianu w licznikach i mianownik.