Różnica między różnicą a pochodną

Aby lepiej zrozumieć różnicę między różnicą a pochodną funkcji, musisz najpierw zrozumieć pojęcie funkcji.

Funkcja jest jedną z podstawowych pojęć z matematyki, która określa związek między zestawem danych wejściowych a zestawem możliwych wyjść, w których każde wejście jest powiązane z jednym wyjściem. Jedna zmienna to zmienna niezależna, a drugą zmienną jest zmienna zależna.

Pojęcie funkcji jest jednym z najbardziej niedocenianych tematów w matematyce, ale jest niezbędna w definiowaniu relacji fizycznych. Weźmy na przykład: stwierdzenie „y jest funkcją x” oznacza, że ​​coś związanego z y jest bezpośrednio związane z x przez jakąś formułę. Powiedzmy, czy wejście to 6, a funkcją jest dodanie 5 do wejścia 6. Wynik to 6+5 = 11, czyli twoje wyjście.

Istnieje kilka wyjątków w matematyce lub można powiedzieć problemy, których nie można rozwiązać zwykłymi metodami geometrii i samej algebry. Nowa gałąź matematyki znana jako rachunek różniczkowy jest używany do rozwiązania tych problemów.

Rachunek zasadniczo różni się od matematyki, która nie tylko wykorzystuje pomysły z geometrii, arytmetyki i algebry, ale także zajmuje się zmianą i ruchem.

Rachunek jako narzędzie określa pochodną funkcji jako granicę konkretnego rodzaju. Pojęcie pochodnej funkcji odróżnia rachunek od innych gałęzi matematyki. Różnica jest podffisją rachunku, które odnosi się do nieskończenie małej różnicy w pewnej różnej ilości i jest jednym z dwóch fundamentalnych podziałów rachunku różniczkowego. Druga gałąź nazywa się rachunkiem integralnym.

Co to jest różnica?

Różnica jest jednym z podstawowych podziałów rachunku różniczkowego, wraz z całkowitym rachunkiem. Jest to podkład rachunku różniczkowego, który zajmuje się nieskończonymi zmianami w pewnej różnej ilości. Świat, w którym żyjemy, jest pełen powiązanych z ilościami, które okresowo się zmieniają.

Na przykład obszar okrągłego ciała, który zmienia się wraz ze zmianami promienia lub pocisku, który zmienia się wraz z prędkością. Te zmieniające się podmioty, w kategoriach matematycznych, są nazywane zmiennymi, a szybkość zmiany jednej zmiennej w odniesieniu do drugiej jest pochodną. A równanie reprezentujące związek między tymi zmiennymi nazywa się równaniem różniczkowym.

Równania różniczkowe to równania zawierające nieznane funkcje i niektóre z ich pochodnych.

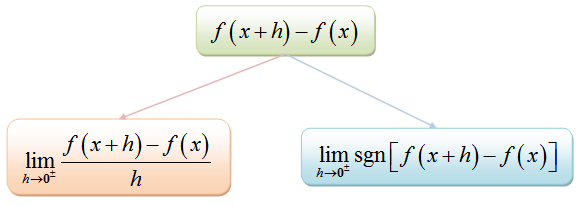
Co to jest pochodne?

Pojęcie pochodnej funkcji jest jedną z najpotężniejszych pojęć w matematyce. Pochodna funkcji jest zwykle nową funkcją, która jest wywoływana jako funkcja pochodna lub funkcja szybkości.

Pochodna funkcji reprezentuje natychmiastową szybkość zmiany wartości zmiennej zależnej w odniesieniu do zmiany wartości zmiennej niezależnej. Jest to podstawowe narzędzie rachunku różniczkowego, które można również interpretować jako nachylenie linii stycznej. Mierzy, jak stromy jest wykres funkcji w pewnym punkcie na wykresie.

Mówiąc prosto, pochodna jest szybkość, z jaką funkcja zmienia się w pewnym konkretnym punkcie.

Różnica między różnicą a pochodną

Definicja różnic vs. Pochodna

Zarówno terminy różnicowe, jak i pochodne są ściśle ze sobą połączone pod względem wzajemnych powiązań. W matematyce zmieniające się jednostki nazywane są zmiennymi, a szybkość zmiany jednej zmiennej w odniesieniu do drugiej nazywana jest pochodną.

Równania, które definiują związek między tymi zmiennymi i ich pochodnymi, nazywane są równaniami różnicznymi. Różnicowanie to proces znajdowania pochodnej. Pochodną funkcji jest szybkość zmiany wartości wyjściowej w odniesieniu do jej wartości wejściowej, podczas gdy różnica to faktyczna zmiana funkcji.

Związek różnicowej vs. Pochodna

Różnicowanie jest metodą obliczania pochodnej, która jest szybkością zmiany wyjścia y funkcji w odniesieniu do zmiany zmiennej x.

Mówiąc prosto, pochodna odnosi się do szybkości zmiany y w odniesieniu do x, a związek ten wyraża się jako y = f (x), co oznacza, że ​​y jest funkcją x. Pochodna funkcji f (x) jest definiowana jako funkcja, której wartość generuje nachylenie f (x), gdzie jest zdefiniowana, a f (x) jest różniczalny. Odnosi się do nachylenia wykresu w danym punkcie.

Reprezentacja różnicowego vs. Pochodna

Różnice są reprezentowane jako DX, Dy, Dt i tak dalej, gdzie Dx reprezentuje niewielką zmianę w x, Dy reprezentuje niewielką zmianę w y i Dt to niewielka zmiana w t. Porównując zmiany w powiązanych ilościach, w których y jest funkcją x, różnicową Dy można napisać jako:

Dy = f^'(X) DX

Pochodną funkcji jest nachylenie funkcji w dowolnym momencie i jest zapisywane jako D/DX. Na przykład pochodną grzechu (x) można zapisać jako:

D/Dx sin (x) = sin (x)^' = cos (x)

Różnicowy vs. Pochodna: wykres porównawczy

Podsumowanie różnic vs. Pochodna

W matematyce szybkość zmiany jednej zmiennej w odniesieniu do innej zmiennej nazywana jest pochodną, ​​a równania, które wyrażają związek między tymi zmiennymi i ich pochodnymi, nazywane są równaniami różnicznymi. W skrócie, równania różnicowe obejmują pochodne, które w rzeczywistości określają, w jaki sposób zmienia się ilość w odniesieniu do innej. Rozwiązując równanie różniczkowe, otrzymujesz wzór dla ilości, która nie zawiera pochodnych. Metoda obliczania pochodnej nazywa się różnicowaniem. Mówiąc prosto, pochodną funkcji jest szybkość zmiany wartości wyjściowej w odniesieniu do jej wartości wejściowej, podczas gdy różnica to faktyczna zmiana funkcji.