Różnica między pracownikiem pracy i asocjacyjnym

Matematyka to gra liczb, a liczby są wszędzie. A zasada gry to właściwości i zasady związane z liczbami. Właściwości pomagają szybko i łatwo obliczyć odpowiedzi w głowie. Nieruchomości to tylko specjalne zasady, które podążają za liczbami. Istnieją trzy podstawowe właściwości liczb, które stosuje każdy system matematyki: właściwości przemienne, asocjacyjne i dystrybucyjne. Te właściwości są cechami czterech operacji (dodaj, odejmij, pomnóż i dziel), które zawsze mają zastosowanie niezależnie od liczby, z którą pracujesz. Ale w następnym artykule omówimy tylko nieruchomości przemienne i asocjacyjne.

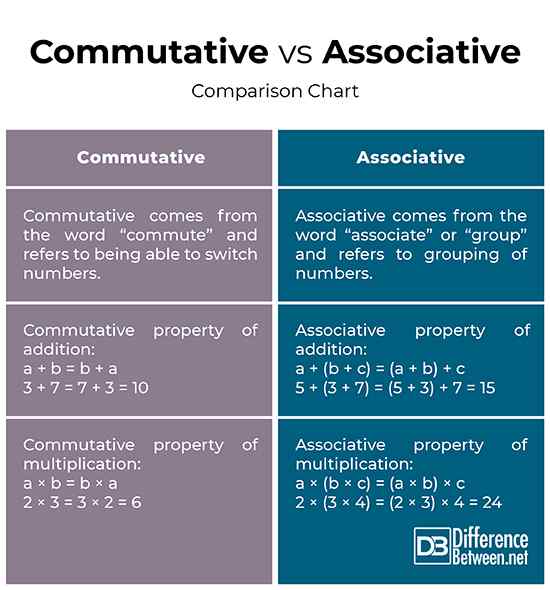
Zarówno właściwości towarzyszące, jak i asocjacyjne są stosowane w zakresie operacji dodawania i mnożenia. Te właściwości są przepisami stosowanymi w algebrze w celu rozwiązania problemów. Własność do pracy pochodzi od terminu „dojazd”, co oznacza poruszanie się i odnosi się do możliwości zmiany liczb, które dodajesz lub mnoż. Własność asocjacyjna pochodzi od słowa „stowarzyszona” lub „grupa” i odnosi się do grupowania trzech lub więcej liczb za pomocą nawiasów, niezależnie od tego, jak je grupujesz. Wynik pozostaje taki sam, bez względu na to, jak zmienisz grupy liczby. Rzućmy okiem na dwie nieruchomości, aby lepiej zrozumieć, jak działają.

Co jest do pracy?

Na przykład; Wiemy, że dodanie 2 i 5 daje taką samą odpowiedź jak dodanie 5 i 2. Kolejność liczb w problemie z dodatkiem można zmienić bez zmiany wyniku. Ta rzecz w liczbach i dodaniu nazywana jest własnością przemienną dodawania. Możemy więc powiedzieć, że dodanie jest operacją przemienną. Podobnie mnożenie jest operacją przemienną.

Przemienność dodawania:

A + B = B + A

3 + 4 = 7 jest taki sam jak 4 + 3 = 7

Wynik będzie taki sam, niezależnie od rzędu liczb.

Własność zamieszania:

A × B = B × a

3 × 7 = 21 jest taki sam jak 7 × 3 = 21

Podobnie wynik będzie taki sam, niezależnie od rzędu liczb.

Co jest asocjacyjnym?

Associative to kolejna właściwość, której używamy, ma związek z ponowną grupą. Na przykład, przy dodaniu 2 + 3 + 5, możemy najpierw dodać 2 i 3. Matematycznie wygląda na to: 2 + 3 + 5 = 2 + (3 + 5) = (2 +3) + 5. Operacje, które zachowują się w ten sposób, nazywane są operacjami asocjacyjnymi. Wynik pozostaje taki sam, nawet jeśli zmienimy grupowanie liczb.

Własność asocjacyjna dodawania:

A + (B + C) = (A + B) + C = A + B + C

1 + (2 +3) = (1 +2) + 3 = 6

Wynik pozostaje taki sam, bez względu na to, jak grupujesz liczby.

Właściwość asocjacyjna mnożenia:

A × (B × C) = (A × B) × C

2 × (3 × 4) = 2 × 12 = 24

(2 × 3) × 4 = 6 × 4 = 24

Tak więc grupa w liczbach nie zmienia wyniku.

Różnica między pracownikiem pracy i asocjacyjnym

Oznaczający

- Własność do pracy pochodzi od terminu „dojeżdżanie do pracy”, co oznacza „poruszanie się” i odnosi się do możliwości zmiany liczb, które dodajesz lub rozmnażasz, niezależnie od kolejności liczb. Z drugiej strony właściwość asocjacyjna pochodzi od słowa „Associate” lub „grupa” i odnosi się do grupowania trzech lub więcej liczb za pomocą nawiasów, niezależnie od tego, jak je grupujesz. Wynik będzie taki sam, bez względu na to, w jaki sposób zmienisz liczby lub zmienne.

Reguła

- Przedstawicielska zasada dodawania stanów, A + B = B + A, co oznacza, że ​​dodanie A i B daje taki sam wynik, jak dodanie B i A. Zamówienia mogą być zmiany bez zmiany wyniku. Ta zasada dodawania nazywana jest własnością przemienną dodawania. Podobnie, mnożenie jest operacją przemienną, co oznacza, że ​​A × B daje taki sam wynik jak B × A. Z drugiej strony właściwość asocjacyjna jest zasadą odnoszącej się do grupowania liczb. Asoodowcina stanów dodawania, a + (b + c) jest taka sama jak (a + b) + c. Podobnie, asocjacyjna zasada mnożenia mówi, że A × (B × C) jest taka sama jak (A × B) × C.

Przykład

- Właściwość komutatywna dodawania: 1 + 2 = 2 +1 = 3

Właściwość komutatywna mnożenia: 2 × 3 = 3 × 2 = 6

Właściwość asocjacyjna dodawania: 5 + (3 + 7) = (5 + 3) + 7 = 15

Właściwość asocjacyjna mnożenia: 5 × (2 × 4) = (5 × 2) × 4 = 40

Przesunięcie vs. Associative: Porównanie wykresu

Streszczenie

Krótko mówiąc, własność przemienna nie ma mylić z własnością asocjacyjną. Własność do pracy stwierdza, że ​​można zmienić kolejność liczb i operacje mnożenia, ponieważ wynik będzie taki sam, bez względu na zamówienie. Z drugiej strony właściwość asocjacyjna stwierdza, że ​​wynik będzie taki sam, bez względu na to, jak grupujesz liczbę lub zmienne operacje dodatkowe/mnożące.