Różnica między rozkładem dwumianowym i poissona

- 4530
- 416
- Emilia Rudziński
 rozkład dwumianowy jest jednym, którego możliwą liczbą wyników jest dwa, tj.mi. sukces lub porażka. Z drugiej strony nie ma limitu możliwych wyników Dystrybucja Poissona
rozkład dwumianowy jest jednym, którego możliwą liczbą wyników jest dwa, tj.mi. sukces lub porażka. Z drugiej strony nie ma limitu możliwych wyników Dystrybucja Poissona
Teoretyczny rozkład prawdopodobieństwa jest zdefiniowany jako funkcja, która przypisuje prawdopodobieństwo każdej możliwej wyniki eksperymentu statystycznego. Rozkład prawdopodobieństwa może być dyskretny lub ciągły, gdzie w dyskretnej zmiennej losowej całkowite prawdopodobieństwo jest przydzielane do różnych punktów masy, podczas gdy w ciągłej zmiennej losowej prawdopodobieństwo jest rozmieszczone w różnych przedziałach klasowych.
Rozkład dwumianowy i rozkład Poissona to dwa dyskretne rozkład prawdopodobieństwa. Rozkład normalny, dystrybucja uczniów, rozkład chi-kwadrat i dystrybucja F to rodzaje ciągłej zmiennej losowej. Tutaj idziemy omówić różnicę między rozkładem dwumianowym a poissonem. Spójrz.
Treść: rozkład dwumianowy vs dystrybucja Poissona
- Wykres porównania
- Definicja
- Kluczowe różnice
- Wniosek
Wykres porównania
| Podstawa do porównania | Rozkład dwumianowy | Dystrybucja Poissona |
|---|---|---|
| Oznaczający | Rozkład dwumianowy to taki, w którym badano prawdopodobieństwo powtarzanej liczby prób. | Rozkład Poissona daje liczbę niezależnych zdarzeń występuje losowo z danym okresem czasu. |
| Natura | Dwuparametryczny | Uniparametryczny |
| Liczba prób | Naprawił | Nieskończony |
| Powodzenie | Stałe prawdopodobieństwo | Nieskończona szansa na sukces |
| Wyniki | Tylko dwa możliwe wyniki, ja.mi. sukces lub porażka. | Nieograniczona liczba możliwych wyników. |
| Średnia i wariancja | Średnia> wariancja | Mean = wariancja |
| Przykład | Eksperyment zrzucania monet. | Błędy drukowania/strona dużej książki. |
Definicja rozkładu dwumianowego
Rozkład dwumianowy jest szeroko stosowanym rozkładem prawdopodobieństwa, pochodzącym z procesu Bernoulli (losowy eksperyment nazwany na cześć znanego matematyka Bernoulli). Jest również znany jako rozkład biparametryczny, ponieważ znajduje się w dwóch parametrach N i P. Tutaj n jest powtarzającymi się próbami, a P to prawdopodobieństwo sukcesu. Jeśli wartość tych dwóch parametrów jest znana, oznacza to, że rozkład jest w pełni znany. Średnia i wariancja rozkładu dwumianowego są oznaczone przez µ = np i σ2 = npq.
P (x = x) = NCX PX QN-X, x = 0,1,2,3… n
= 0, w przeciwnym razie
Próba danego wyniku, który wcale nie jest pewien i niemożliwy, nazywa się próbą. Próby są niezależne i stałą liczbę całkowitą. Jest to związane z dwoma wzajemnie wykluczającymi się i wyczerpującymi zdarzeniami; w którym występowanie nazywa się sukcesem, a brak występowania nazywane jest porażką. P reprezentuje prawdopodobieństwo sukcesu, podczas gdy q = 1 - p reprezentuje prawdopodobieństwo awarii, co nie zmienia się w całym procesie.
Definicja rozkładu Poissona
Pod koniec lat 30. XIX wieku słynny francuski matematyk Simon Denis Poisson wprowadził ten rozkład. Opisuje prawdopodobieństwo pewnej liczby zdarzeń występujących w ustalonym przedziale czasowym. Jest to rozkład jednoparametryczny, ponieważ jest opisany tylko jednym parametrem λ lub m. W Poissona średnia rozkładu jest oznaczona przez M i.mi. µ = m lub λ, a wariancja jest oznaczona jako σ2 = m lub λ. Funkcja masy prawdopodobieństwa x jest reprezentowana przez:
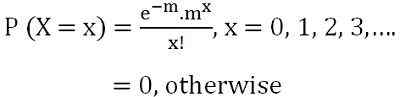 gdzie E = ilość transcendentalna, której przybliżona wartość wynosi 2.71828
gdzie E = ilość transcendentalna, której przybliżona wartość wynosi 2.71828
Gdy liczba zdarzeń jest wysoka, ale prawdopodobieństwo jego wystąpienia jest dość niskie, zastosowano rozkład Poissona. Jak na przykład liczba roszczeń ubezpieczeniowych/dzień w firmie ubezpieczeniowej.
Kluczowe różnice między rozkładem dwumianowym i Poissona
Różnice między rozkładem dwumianowym i Poissona można wyraźnie wyciągnąć na następujących podstawach:
- Rozkład dwumianowy to taki, w którym badano prawdopodobieństwo powtarzanej liczby prób. Rozkład prawdopodobieństwa, który daje liczbę niezależnych zdarzeń, występuje losowo w danym okresie, nazywa się rozkładem prawdopodobieństwa.
- Rozkład dwumianowy jest biparametryczny, i.mi. Jest przedstawiony przez dwa parametry N i P, podczas gdy rozkład Poissona jest uniparametryczny, i.mi. charakteryzujący się pojedynczym parametrem m.
- Istnieje ustalona liczba prób rozkładu dwumianowego. Z drugiej strony nieograniczona liczba prób jest w dystrybucji Poissona.
- Prawdopodobieństwo sukcesu jest stałe w rozmieszczeniu dwumianowym, ale w dystrybucji Poissona istnieje wyjątkowo niewielka liczba szans sukcesu.
- W rozmieszczeniu dwumianowym istnieją tylko dwa możliwe wyniki, i.mi. sukces lub porażka. I odwrotnie, istnieje nieograniczona liczba możliwych wyników w przypadku dystrybucji Poissona.
- W średniej rozkładu dwumianowego> wariancja podczas średniej rozkładu Poissona = wariancja.
Wniosek
Oprócz powyższych różnic istnieje wiele podobnych aspektów między tymi dwoma rozkładami i.mi. Oba są dyskretnym teoretycznym rozkładem prawdopodobieństwa. Ponadto, na podstawie wartości parametrów, oba mogą być jednorodne lub bimodalne. Ponadto rozkład dwumianowy może być aproksymowany przez rozkład Poissona, jeżeli liczba prób (n) ma tendencję do prawdopodobieństwa nieskończoności i sukcesu (p), więc M = np.

