Różnica między średnią a medianą
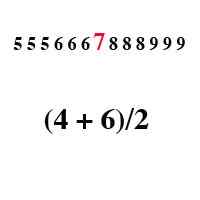
- 1438
- 5
- Emilia Rudziński
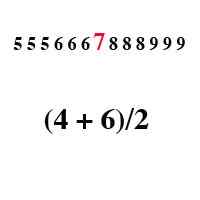 Średnia vs mediana
Średnia vs mediana
Mediana to liczba reprezentująca ã „środkową próbkę danych, która została ułożona numerycznie, biorąc pod uwagę, że próbka liczb jest dziwna po zliwieniu. W przypadku zbioru danych, który jest nawet liczby po zliwieniu, mediana w tym przypadku zostanie uzyskana poprzez podzielenie suma dwóch średnich liczb przez 2. Statystyka i teoria prawdopodobieństwa opisuje medianę jako wartość liczbową, która dzieli próbkę na dwie równe połówki, czyli dolna połowa i wyższa połowa. Zestaw danych obejmuje między innymi próbkę i populację.
W dowolnej próbce wyższa połowa będzie się co najwyżej składać z wartości większych niż mediana, podczas gdy dolna połowa będzie składać się z wartości mniejszych niż mediana. Jeśli oba połowy mają mniej niż połowę próbki, będzie to oznaczać, że część próbki będzie dokładnie równa medianie. Weźmy na przykład, jeśli x < z, then y will be the median of the sample x, y, z and if x < z
Mediana można czasami stosować do przedstawienia miary lokalizacji, w której rozkład jest ukośny, gdy ostatnie wartości nie są znane lub gdy wartości zewnętrzne nie są ważne, jeśli na przykład mogą spowodować błędy pomiaru. Teoretycznie mediana jest bardzo trudna w obsłudze i jest to główna wada.
Średnia jest zwykle (i błędnie) określana jako średnia, ale średnia nie zawsze jest równa średniej. Ã „wspólna średnia to ta zwana średnia, ale zdecydowanie średnia nie oznacza znaczenia.
Z praktycznego punktu widzenia istnieje tylko marginalna różnica między medianą a średnim dla danej próbki, teoretycznie, różnice mogą być surowe. Jednym z głównych faktów jest to, że różnicy między nimi nie można łatwo zrozumieć i jest powszechnym źródłem zamieszania dla wielu osób. Zatem słowo „średnie jest często używane, gdy w rzeczywistości informacje miało reprezentować tryb lub medianę.
Streszczenie
Mediana jest środkową liczbą danego zestawu danych (jeśli jest to dziwne), podczas gdy średnia jest definicją środki arytmetycznej, która jest najczęściej cytowaną średnią.
Wartość mediany zależy od liczby elementów w zestawie danych (nieparzyste lub nawet), podczas gdy średnia nie.

