Różnica między ASA i AAS

ASA vs AAS: ASA oznacza „kąt, bok, kąt”, podczas gdy AAS oznacza „kąt, kąt, bok”

Geometria jest zabawna. Geometria dotyczy kształtów, rozmiarów i wymiarów. Geometria jest rodzajem matematyki, która dotyczy badania kształtów. Łatwo zrozumieć, dlaczego geometria ma tak wiele aplikacji, które odnoszą się do prawdziwego życia. Jest używany we wszystkim - w inżynierii, architekturze, sztuce, sporcie i wielu innych. Dzisiaj omówimy geometrię trójkąta, w szczególności zgodność trójkąta. Ale najpierw musimy zrozumieć, co to znaczy być przystającym. Dwie postacie są zgodne, jeśli jedna można przenieść na drugą w taki sposób, że wszystkie ich części się pokrywają. Innymi słowy, dwie postacie nazywane są przystającymi, jeśli mają ten sam kształt i rozmiar. Dwie przystające postacie to jedna i ta sama liczba, w dwóch różnych miejscach.

To prawda niż zgodność trójkąta jest podstawowym elementem budowy wielu koncepcji i dowodów geometrycznych. Trójkąta zgodność jest jedną z najczęstszych koncepcji geometrycznych w studiach średnich. Jedną główną koncepcją często pomijaną w nauczaniu i uczeniu się o zgodności trójkąta jest koncepcja wystarczalności, to znaczy ustalenie warunków, które spełniają, że dwa trójkąty są zgodne. Istnieje pięć sposobów ustalenia, czy dwa trójkąty są zgodne, ale omówimy tylko dwa, to znaczy ASA i AAS. ASA oznacza „kąt, bok, kąt”, podczas gdy AAS oznacza „kąt, kąt, bok”. Przyjrzyjmy się, jak użyć tych dwóch, aby ustalić, czy dwa trójkąty są zgodne.

Co to jest zgodność trójkąta ASA?

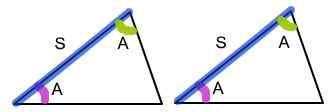
ASA oznacza „kąt, bok, kąt”, co oznacza, że ​​dwa trójkąty są zgodne, jeśli mają równą stronę zawartą między odpowiednimi równymi kątami. Jeśli wierzchołki dwóch trójkątów są w korespondencji jeden do jednego tak, że dwa kąty i uwzględniona strona jednego trójkąta są odpowiednio zgodne z dwoma kątami i uwzględnioną stroną drugiego trójkąta, wówczas spełnia warunek, że jest to, że jest to warunek, że jest to warunek, że jest to warunek, że jest to warunek, że spełnia warunek. Trójkąty są przystające. Ponieważ dwa kąty i uwzględniona strona są równe w obu trójkątach, trójkąty są nazywane przystającym.

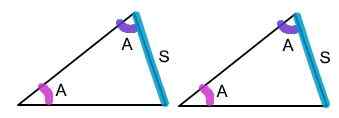
Co to jest zgodność trójkąta AAS?

AAS oznacza „kąt, kąt, bok”, co oznacza dwa kąty i przeciwną stronę. AAS jest jednym z pięciu sposobów ustalenia, czy dwa trójkąty są przystające. Stwierdza, że ​​jeśli wierzchołki dwóch trójkątów są w korespondencji jeden do jednego, tak że dwa kąty i strona przeciwna do jednego z nich w jednym trójkącie są zgodne z odpowiednimi kątami i nie zakłóconą stroną drugiego trójkąta, wówczas trójkąty są przystające. Strona nieinklude jest stroną przeciwną do jednego z dwóch stosowanych kąta. Mówiąc prosto, jeśli dwie pary odpowiednich kąty i strony przeciwne do nich są równe w obu trójkątach, dwa trójkąty są zgodne.

Różnica między ASA i AAS

Terminologia ASA i AAS

- ASA i AA są dwoma postulatami, które pomagają nam ustalić, czy dwa trójkąty są zgodne. ASA oznacza „kąt, bok, kąt”, podczas gdy AAS oznacza „kąt, kąt, bok”. Dwie postacie są zgodne, jeśli mają ten sam kształt i rozmiar. Innymi słowy, dwie przystające postacie to jedna i ta sama liczba, w dwóch różnych miejscach. Podczas gdy oba są terminami geometrii używanymi w dowodach i odnoszą się do umieszczenia kąty i stron, różnica polega na tym, kiedy ich użyć. ASA odnosi się do dowolnych dwóch kąty i uwzględnionej strony, podczas gdy AAS odnosi się do dwóch odpowiadających kąt.

Stosowność

- Według zgodności ASA dwa trójkąty są zgodne, jeśli mają one równą stronę zawartą między odpowiednimi równymi kątami. Innymi słowy, jeśli dwa kąty i uwzględniona strona jednego trójkąta są równe odpowiednim kątach i uwzględnionej stronie drugiego trójkąta, wówczas dwa trójkąty są nazywane przysłami, zgodnie z zasadą ASA, zgodnie z zasadą ASA. Z drugiej strony reguła AAS stwierdza, że ​​jeśli wierzchołki dwóch trójkątów są w korespondencji jeden do jednego, tak że dwa kąty i strona przeciwna do jednego z nich w jednym trójkącie są równe odpowiednim kątom i nie- Włączono stronę drugiego trójkąta, wówczas trójkąty są przystające.

Reprezentacja

- Główną różnicą między dwiema zasadami zgodności jest to, że strona jest zawarta w postulatu ASA, podczas gdy strona nie jest uwzględniona w postulatie AAS.

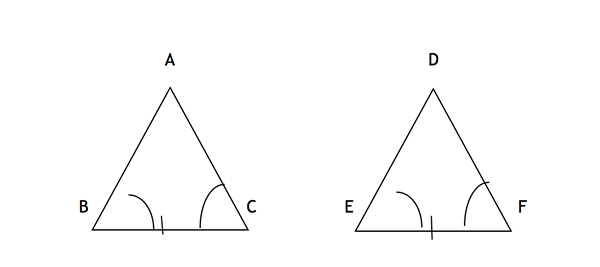
Tutaj dwa kąty (ABC i ACB) i dołączona strona (BC) są zgodne z odpowiednimi kątami (Def i DFE), a jedna uwzględniona strona (EF), która sprawia, że ​​dwa trójkąty są zgodne, zgodnie z zasadą zgodności ASA, zgodnie z zasadą zgodności ASA.

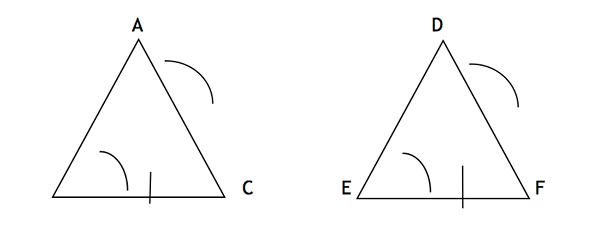
Tutaj dwa kąty (ABC i BAC) i jedna nie zakłócona strona (BC) pierwszego trójkąta są zgodne z odpowiednimi kątami (def i EDF) oraz niezwiązaną stroną (EF) drugiego trójkąta, co czyni The the the the drugiego trójkąta, co czyni The the the drugiego trójkąta, co czyni The the Drugi trójkąt, co czyni The the the Drug Triangle Dwa trójkąty przystające. AC i EF mogą być również niezaprzeczonymi stronami odpowiednio dwóch trójkątów.

ASA vs. AAS: wykres porównawczy

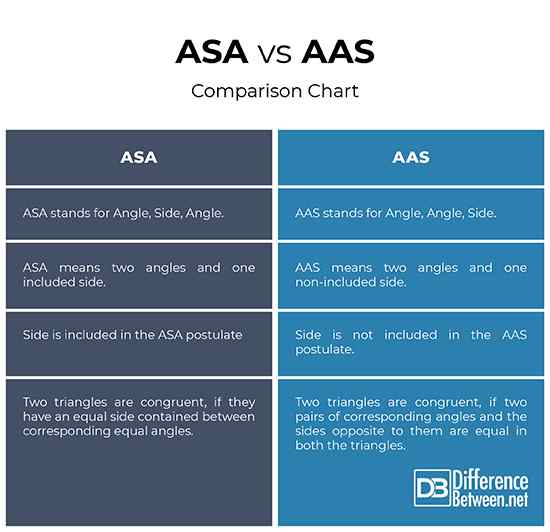
Podsumowanie ASA vs. Aas

Krótko mówiąc, ASA i AA są dwiema z pięciu zasad zgodności, które określają, czy dwa trójkąty są zgodne. ASA oznacza „kąt, bok, kąt”, co oznacza, że ​​dwa trójkąty są zgodne, jeśli mają równą stronę zawartą między odpowiednimi równymi kątami. AA odnosi się do „kąt, kąt, bok”, co oznacza, że ​​jeśli dwie pary odpowiadających kątów i boki przeciwne do nich są równe w obu trójkątach, dwa trójkąty są nazywane przystającym. Chociaż oba są zasadniczo takie same, główną różnicą między dwiema zasadami zgodności jest to, że strona jest zawarta w regule ASA, podczas gdy strona nie jest uwzględniona w regule AAS.