Różnice między korelacją a regresją

Zarówno korelacja, jak i regresja są narzędziami statystycznymi, które dotyczą dwóch lub więcej zmiennych. Chociaż oba odnoszą się do tego samego tematu, istnieją różnice między nimi. Różnice między nimi są wyjaśnione poniżej.

Oznaczający

Termin korelacja w odniesieniu do dwóch lub więcej zmiennych oznacza, że ​​zmienne są w jakiś sposób powiązane. Analiza korelacji określa, czy istnieje związek między dwiema zmiennymi, a siła relacji. Jeżeli dwie zmienne x (niezależne) i y (zależne) są tak powiązane, że zmienność zmiennej niezależnej towarzyszy, zmienność wielkości zmiennej zależnej, wówczas mówi się, że dwie zmienne są skorelowane.

Korelacja może być liniowa lub nieliniowa. Korelacja liniowa to taka, w której zmienne są tak powiązane, że zmiana wartości jednej zmiennej spowodowałaby konsekwentnie zmianę wartości innej zmiennej. W korelacji liniowej rozproszone punkty związane z odpowiednimi wartościami zmiennych zależnych i niezależnych skupiałyby się wokół niehoryzontalnej linii prostej, chociaż pozioma linia prosta wskazywałaby również na liniową zależność między zmiennymi, gdyby linia prosta mogłaby połączyć punkty reprezentujące zmienne.

Z drugiej strony analiza regresji wykorzystuje istniejące dane do określenia matematycznego związku między zmiennymi, które można użyć do określenia wartości zmiennej zależnej w odniesieniu do dowolnej wartości zmiennej niezależnej.

Orientacja statystyczna

Korelacja dotyczy pomiaru siły asocjacji lub intensywności relacji, gdzie jako regresja dotyczy przewidywania wartości zmiennej zależnej w stosunku do znanej wartości zmiennej niezależnej. Można to wyjaśnić następującymi formułami.

Współczynnik korelacji lub korelacja współczynnika (R) między X & Y znajduje się z następującym wzorem;

r = kowariancja (x, y)/σx.σy, Cov (x, y) = σxy/n - (σx/n) (σy/n), σx i σy są standardowymi odchyleniami x i y i -1 i -1 < r 0, then correlation coefficient between x and y = correlation coefficient between u and v.

Współczynnik korelacji R jest czystą liczbą i niezależną od jednostki pomiaru. Zatem jeśli x jest wysokością (cale), a y ma wagę (lbs.) ludzi z określonego regionu, wówczas R nie jest w calach, ani w lbs., Ale po prostu liczba.

Równanie regresji znajduje się w następującym wzorze;

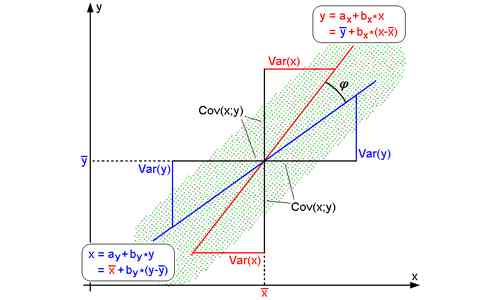
Równanie regresji y na x (aby znaleźć oszacowanie y) to y - y '= byx (x -x‾), BYX nazywa się współczynnikiem regresji y na x. Równanie regresji x na y (aby znaleźć oszacowanie x) to x - x '= bxy (y -y‾), bxy nazywa się współczynnikiem regresji x na y.

Analiza korelacji nie zakłada zależności jakiejkolwiek zmiennej od innej zmiennej, nie próbuje też znaleźć związku między nimi. Po prostu szacuje stopień związku między zmiennymi. Innymi słowy, analiza korelacji testuje współzależność zmiennych. Analiza regresji z drugiej strony opisuje zależność zmiennej zależnej lub zmiennej odpowiedzi od zmiennej niezależnej lub objaśniającej/s/s. Analiza regresji zakłada, że ​​istnieje jednokierunkowy związek przyczynowy między zmiennymi objaśniającymi i reakcyjnymi i nie bierze pod uwagę tego, czy związek przyczynowy jest pozytywny czy negatywny. Dla korelacji zarówno wartości zmiennych zależnych, jak i niezależnych są losowe, ale dla wartości regresji zmiennych niezależnych nie muszą być losowe.

Streszczenie

1. Analiza korelacji jest testem wzajemnej zależności między dwiema zmiennymi. Analiza regresji podaje wzór matematyczny w celu ustalenia wartości zmiennej zależnej w odniesieniu do wartości zmiennej niezależnej/s.

2. Współczynnik korelacji jest niezależny od wyboru pochodzenia i skali, ale współczynnik regresji nie jest tak.

Dla korelacji wartości obu zmiennych muszą być losowe, ale nie jest to tak dla współczynnika regresji.

Bibliografia

1. Das, n. G., (1998), Metody statystyczne, Kalkuta

2. Korelacja i regresja, dostępne na stronie www.le.AC.UK/BL/GAT/VirtualFC/Stats/Regress

3. Regresja i korelacja, dostępne na stronie WWW.przepaść.Uoregon.Edu