Różnica między wariancją a odchyleniem standardowym

- 4022
- 732
- Pani — Jóźwiak
 Dyspersja wskazuje, w jakim stopniu obserwacje odbiegają od odpowiedniej miary tendencji centralnej. Środki dyspersji dzielą się na dwie kategorie I.mi. bezwzględna miara dyspersji i względna miara dyspersji. Wariancja i odchylenie standardowe to dwa typy bezwzględnej miary zmienności; który opisuje, w jaki sposób obserwacje są rozłożone wokół średniej. Zmienność to nic innego jak średnia kwadratów odchyleń,
Dyspersja wskazuje, w jakim stopniu obserwacje odbiegają od odpowiedniej miary tendencji centralnej. Środki dyspersji dzielą się na dwie kategorie I.mi. bezwzględna miara dyspersji i względna miara dyspersji. Wariancja i odchylenie standardowe to dwa typy bezwzględnej miary zmienności; który opisuje, w jaki sposób obserwacje są rozłożone wokół średniej. Zmienność to nic innego jak średnia kwadratów odchyleń,
w odróżnieniu, odchylenie standardowe jest pierwiastkiem kwadratowym uzyskanej wartości numerycznej podczas obliczania wariancji. Wiele osób kontrastuje te dwa koncepcje matematyczne. Tak więc ten artykuł próbuje rzucić światło na ważną różnicę między wariancją a odchyleniem standardowym.
Treść: wariancja vs odchylenie standardowe
- Wykres porównania
- Definicja
- Kluczowe różnice
- Ilustracja
- Podobieństwa
- Wniosek
Wykres porównania
| Podstawa do porównania | Zmienność | Odchylenie standardowe |
|---|---|---|
| Oznaczający | Wariancja jest wartością liczbową, która opisuje zmienność obserwacji ze swojej średniej arytmetycznej. | Odchylenie standardowe jest miarą rozproszenia obserwacji w zestawie danych. |
| Co to jest? | Jest to średnia kwadratowych odchyleń. | Jest to średnie odchylenie kwadratowe. |
| Oznaczone jako | Sigma-kwadrat (σ^2) | Sigma (σ) |
| Wyrażone w | Kwadratowe jednostki | Te same jednostki, co wartości w zestawie danych. |
| Wskazuje | Jak daleko rozpowszechniane są jednostki w grupie. | Ile obserwacji zestawu danych różni się od jego średniej. |
Definicja wariancji
W statystykach wariancja jest zdefiniowana jako miara zmienności, która reprezentuje rozkładanie członków grupy. Dowiaduje się o średnim stopniu, w jakim każda obserwacja różni się od średniej. Gdy wariancja zestawu danych jest niewielka, pokazuje bliskość punktów danych do średniej, podczas gdy większa wartość wariancji reprezentuje, że obserwacje są bardzo rozproszone wokół średniej arytmetycznej i od siebie nawzajem.
Dla danych niesklasyfikowanych: 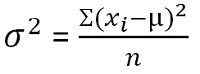
Dla zgrupowanego rozkładu częstotliwości: 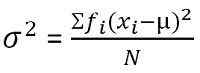
Definicja odchylenia standardowego
Odchylenie standardowe jest miarą, która kwantyfikuje ilość dyspersji obserwacji w zestawie danych. Niskie odchylenie standardowe jest wskaźnikiem bliskości wyników do średniej arytmetycznej i reprezentuje wysokie odchylenie standardowe; Wyniki są rozproszone w wyższym zakresie wartości.
Dla danych niesklasyfikowanych: 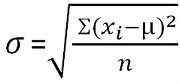 Dla zgrupowanego rozkładu częstotliwości:
Dla zgrupowanego rozkładu częstotliwości: 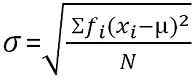
Kluczowe różnice między wariancją a odchyleniem standardowym
Różnica między odchyleniem standardowym a wariancją można wyraźnie narysować na następujących podstawach:
- Wariancja jest wartością liczbową, która opisuje zmienność obserwacji ze swojej średniej arytmetycznej. Odchylenie standardowe jest miarą dyspersji obserwacji w zestawie danych w stosunku do ich średniej.
- Wariancja jest niczym innym jak średnią odchyleń kwadratowych. Z drugiej strony, odchylenie standardowe jest średniego kwadratu korzeniowego.
- Wariancja jest oznaczona przez sigma-kwadrat (σ2) Podczas gdy odchylenie standardowe jest oznaczone jako Sigma (σ).
- Wariancja jest wyrażona w jednostkach kwadratowych, które są zwykle większe niż wartości w danym zestawie danych. W przeciwieństwie do odchylenia standardowego wyrażonego w tych samych jednostkach, co wartości w zestawie danych.
- Wariancja mierzy sposób rozkładu osób w grupie w zestawie danych od średniej. I odwrotnie, odchylenie standardowe mierzy, ile obserwacji zestawu danych różni się od jego średniej.
Ilustracja
Znaki zdobyte przez studenta w pięciu osobach to odpowiednio 60, 75, 46, 58 i 80. Musisz znaleźć odchylenie standardowe i wariancję.
Po pierwsze, musisz dowiedzieć się o średniej,
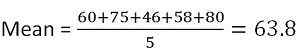
Tak więc średnie (średnie) znaki wynoszą 63.8
Teraz oblicz wariancję
| X | A | (X-A) | (X-a)^2 |
|---|---|---|---|
| 60 | 63.8 | -3.8 | 14.44 |
| 75 | 63.8 | 11.2 | 125.44 |
| 46 | 63.8 | -17.8 | 316.84 |
| 58 | 63.8 | 5.8 | 33.64 |
| 80 | 63.8 | 16.2 | 262.44 |
Gdzie, x = obserwacje
A = średnia arytmetyczna
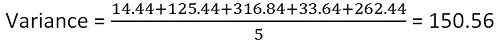 Więc wariancja wynosi 150.56
Więc wariancja wynosi 150.56
A odchylenie standardowe jest - 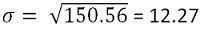
Podobieństwa
- Zarówno wariancja, jak i odchylenie standardowe są zawsze pozytywne.
- Jeśli wszystkie obserwacje w zbiorze danych są identyczne, odchylenie standardowe i wariancja wyniesie zero.
Wniosek
Te dwa są podstawowymi terminami statystycznymi, które odgrywają istotną rolę w różnych sektorach. Odchylenie standardowe jest preferowane niż średnia, ponieważ jest wyrażana w tych samych jednostkach, co oddziaływanie pomiarów, podczas gdy wariancja jest wyrażona w jednostkach większych niż podany zestaw danych.

