Różnica między odchyleniem standardowym a błędem standardowym

- 4691
- 996
- Patrycy Ziółkowski
 Odchylenie standardowe jest zdefiniowany jako bezwzględna miara dyspersji serii. Wyjaśnia standardową ilość zmienności po obu stronach średniej. Często jest źle interpretowane z błędem standardowym, ponieważ opiera się na odchyleniu standardowym i wielkości próbki.
Odchylenie standardowe jest zdefiniowany jako bezwzględna miara dyspersji serii. Wyjaśnia standardową ilość zmienności po obu stronach średniej. Często jest źle interpretowane z błędem standardowym, ponieważ opiera się na odchyleniu standardowym i wielkości próbki.
Standardowy błąd służy do pomiaru dokładności statystycznej oszacowania. Jest stosowany przede wszystkim w procesie testowania hipotezy i szacowania interwału.
Są to dwa ważne pojęcia statystyki, które są szeroko stosowane w dziedzinie badań. Różnica między odchyleniem standardowym a błędem standardowym opiera się na różnicy między opisem danych a ich wnioskiem.
Treść: Odchylenie standardowe w porównaniu do błędu standardowego
- Wykres porównania
- Definicja
- Kluczowe różnice
- Wniosek
Wykres porównania
| Podstawa do porównania | Odchylenie standardowe | Standardowy błąd |
|---|---|---|
| Oznaczający | Odchylenie standardowe implikuje miarę dyspersji zestawu wartości od ich średniej. | Błąd standardowy oznacza miarę dokładności statystycznej oszacowania. |
| Statystyczny | Opisowy | Wnioskowanie |
| Środki | Ile obserwacji różni się od siebie. | Jak precyzyjna oznacza próbka dla prawdziwej populacji. |
| Dystrybucja | Rozkład obserwacji dotyczącej krzywej normalnej. | Rozkład oszacowania dotyczący krzywej normalnej. |
| Formuła | Pierwiastek kwadratowy wariancji | Odchylenie standardowe podzielone przez pierwiastek kwadratowy o wielkości próbki. |
| Wzrost wielkości próby | Daje bardziej specyficzną miarę odchylenia standardowego. | Zmniejsza błąd standardowy. |
Definicja odchylenia standardowego
Odchylenie standardowe, jest miarą rozprzestrzeniania się serii lub odległości od standardu. W 1893 r. Karl Pearson wymyślił pojęcie odchylenia standardowego, które jest niewątpliwie najczęściej stosowane miary, w badaniach naukowych.
Jest to pierwiastek kwadratowy średniej kwadratów odchyleń od ich średniej. Innymi słowy, w przypadku danego zestawu danych odchyleniem standardowym jest decydowanie o powierzchni głównej kwadratowej, od średniej arytmetycznej. Dla całej populacji jest to wskazane przez grecką literę „sigma (σ)”, a dla próbki jest reprezentowana przez łacińską literę „s”.
Odchylenie standardowe jest miarą, która kwantyfikuje stopień rozproszenia zestawu obserwacji. Im dalej punkty danych od wartości średniej, tym większe jest odchylenie w zbiorze danych, reprezentując, że punkty danych są rozproszone w szerszym zakresie wartości i odwrotnie.
- W przypadku danych niesklasyfikowanych:
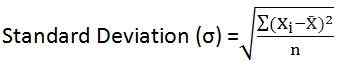
- Dla zgrupowanego rozkładu częstotliwości:

Definicja błędu standardowego
Być może zauważyłeś, że różne próbki o identycznej wielkości, pochodzące z tej samej populacji, dadzą różnorodne wartości rozważanych statystyk, i.mi. średnia próbka. Błąd standardowy (SE) zapewnia odchylenie standardowe w różnych wartościach średniej próbki. Służy do porównania średnich próbek w populacjach.
Krótko mówiąc, standardowy błąd statystyki jest tylko standardowym odchyleniem rozkładu próbkowania. Ma wielką rolę do odgrywania testowania hipotezy statystycznej i oceny przedziałów. Daje wyobrażenie o dokładności i niezawodności oszacowania. Im mniejszy błąd standardowy, tym większa jest jednolitość rozkładu teoretycznego i odwrotnie.
- Formuła: Błąd standardowy dla średniej próbki = σ/√n
Gdzie σ jest odchyleniem standardowym populacji
Kluczowe różnice między odchyleniem standardowym a błędem standardowym
Punkty podane poniżej są znaczne, jeśli chodzi o różnicę między odchyleniem standardowym:
- Odchylenie standardowe to miara, która ocenia ilość zmienności w zestawie obserwacji. Błąd standardowy ocenia dokładność oszacowania, i.mi. jest to miara zmienności rozkładu teoretycznego statystyki.
- Odchylenie standardowe jest statystyką opisową, podczas gdy błąd standardowy jest statystyką wnioskowania.
- Odchylenie standardowe mierzy, jak daleko są poszczególne wartości od wartości średniej. Wręcz przeciwnie, jak blisko jest średnia próbka dla populacji.
- Odchylenie standardowe to rozkład obserwacji w odniesieniu do krzywej normalnej. W związku z tym błąd standardowym jest rozkład oszacowania w odniesieniu do krzywej normalnej.
- Odchylenie standardowe jest definiowane jako pierwiastek kwadratowy wariancji. I odwrotnie, błąd standardowy jest opisany jako odchylenie standardowe podzielone przez pierwiastek kwadratowy o wielkości próbki.
- Po podniesieniu wielkości próby zapewnia bardziej szczególną miarę odchylenia standardowego. W przeciwieństwie do błędu standardowego po zwiększeniu wielkości próbki, błąd standardowy ma tendencję do zmniejszania.
Wniosek
Ogólnie rzecz biorąc, odchylenie standardowe jest uważane za jedno z najlepszych miar dyspersji, które ocenia rozproszenie wartości z wartości centralnej. Z drugiej strony błąd standardowy służy głównie do sprawdzenia niezawodności i dokładności oszacowania, a tym mniejszym błędem, tym większa jest jego niezawodność i dokładność.

