Różnica między sekwencją a serią

- 2013
- 553
- Łukasz Kalisz
 W matematyce i statystykach linia, która wyznacza sekwencję i serie, jest cienka i zamazana, z czego wielu uważa, że te terminy są jednym i to samo. Niemniej jednak pojęcie sekwencji różni się od serii w tym sensie sekwencja odnosi się do porozumienia w konkretnej kolejności, w której powiązane warunki śledzą się nawzajem, i.mi. Ma zidentyfikowaną pierwszą jednostkę, drugą jednostkę, trzecią jednostkę i tak dalej.
W matematyce i statystykach linia, która wyznacza sekwencję i serie, jest cienka i zamazana, z czego wielu uważa, że te terminy są jednym i to samo. Niemniej jednak pojęcie sekwencji różni się od serii w tym sensie sekwencja odnosi się do porozumienia w konkretnej kolejności, w której powiązane warunki śledzą się nawzajem, i.mi. Ma zidentyfikowaną pierwszą jednostkę, drugą jednostkę, trzecią jednostkę i tak dalej.
Gdy sekwencja podąża za konkretną regułą, nazywa się ją progresją. To nie jest dokładnie takie samo jak seria który jest zdefiniowany jako podsumowanie elementów sekwencji. Przeczytaj artykuł, aby poznać znaczącą różnicę między sekwencją a serią.
Treść: Seria sekwencji vs
- Wykres porównania
- Definicja
- Kluczowe różnice
- Wniosek
Wykres porównania
| Podstawa do porównania | Sekwencja | Seria |
|---|---|---|
| Oznaczający | Sekwencja jest opisana jako zestaw liczb lub obiektów, który podąża za określonym wzorem. | Seria odnosi się do sumy elementów sekwencji. |
| Zamówienie | Ważny | Czasami ważne |
| Przykład | 1, 3, 5, 7, 9, 11… n… | 1 + 3 + 5 + 9 + 11… N… |
Definicja sekwencji
W matematyce uporządkowany zestaw obiektów lub liczb, jak1, A2, A3, A4, A5, A6… AN… . Mówi się, że znajdują się w sekwencji, jeśli zgodnie z pewną zasadą ma określoną wartość. Członkowie sekwencji nazywane są terminem lub elementem, który jest równy dowolnej wartości liczby naturalnej. Każdy termin w sekwencji jest związany z poprzednim i kolejnym terminem. Zasadniczo sekwencje mają ukryte reguły lub wzór, co pomaga znaleźć wartość następnego terminu.
N -ten termin jest funkcją liczby całkowitej n (dodatniej), uważanej za ogólny termin sekwencji. Sekwencja może być skończona lub nieskończona.
- Sekwencja skończona: Sekwencja skończona to taka, która zatrzymuje się na końcu listy liczb A1, A2, A3, A4, A5, A6… AN, jest reprezentowany przez:
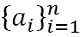
- Sekwencja nieskończona: Nieskończona sekwencja odnosi się do sekwencji, która jest niekończąca się, a1, A2, A3, A4, A5, A6… AN… .., jest reprezentowany przez:
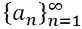
Definicja serii
Dodanie warunków sekwencji (aN), jest znany jako seria. Podobnie jak sekwencja, seria może być również skończona lub nieskończona, gdzie seria skończona jest taka, która ma skończoną liczbę terminów napisanych jako1 + A2 + A3 + A4 + A5 + A6 + … AN. W przeciwieństwie do serii Infinite, w których liczba elementów nie jest skończona lub które są niekończące się, napisane jako1 + A2 + A3 + A4 + A5 + A6 + … AN +… .
Jeśli1 + A2 + A3 + A4 + A5 + A6 + … AN = SN, Następnie sN jest uważany za sumę n elementów serii. Suma terminów jest często reprezentowana przez grecką literę Sigma (ʃ). Stąd,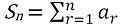
Kluczowe różnice między sekwencją i serią
Różnica między sekwencją a serią można wyraźnie narysować na następujących podstawach:
- Sekwencja jest zdefiniowana jako zbiór liczb lub obiektów, które podążają za określonym wzorem. Gdy elementy sekwencji są dodawane, są one znane jako seria.
- Zamów ma znaczenie w sekwencji, ponieważ istnieje pewna zasada, która określa wzór sekwencji. Stąd 1, 2, 3 -tle różni się od 3, 1, 2. Z drugiej strony, w kolejności wyglądu serii może, ale nie musi, podobnie jak w przypadku absolutnie zbieżnej serii, zamówienie nie ma znaczenia. Tak więc 1 + 2 + 3 jest taki sam jak 3 + 1 + 2, tylko ich sekwencja jest inna.
Wniosek
Postęp arytmetyczny (a.P.) i progresja geometryczna (g.P.) są również sekwencjami, a nie seriami. Postęp arytmetyczny jest sekwencją, w której istnieje powszechna różnica między kolejnymi terminami, takimi jak 2, 4, 6, 8 i tak dalej. Przeciwnie, w postępie geometrycznym każdy element sekwencji jest wspólną wielokrotnością poprzedniego terminu, takiego jak 3, 9, 27, 81 i tak dalej. Podobnie sekwencja Fibonacciego jest również jedną z popularnej nieskończonej sekwencji, w której każdy termin jest uzyskiwany przez dodanie dwóch poprzednich terminów 1, 1, 3, 5, 8, 13, 21 i tak dalej.

